Conocimientos previos
Cuadrado - Rectángulo
Nivel requerido al alumnado
Medio
Interacción
Individual - Pequeño grupo
Características del applet
Tipo de applet
Introducir conceptos
Autocorregible
No
Incluye preguntas
Si
Recomendaciones para su uso en el aula
Trabajo individual
Propuestas para su uso en el aula
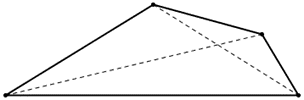
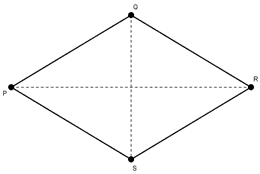
Los cuadriláteros son polígonos convexos de cuatro lados. En este recurso se presenta un estudio de los cuadriláteros atendiendo a sus lados, diagonales y ángulos.
Se pueden clasificar de varias formas según sus características y propiedades.
* Según sus lados:
- Paralelogramos: Tienen los lados opuestos paralelos. Incluyen el cuadrado, el rectángulo, el rombo y el romboide.
- Trapecios: Tienen al menos un par de lados paralelos.
* Según sus ángulos:
- Rectángulos: Tienen cuatro ángulos rectos.
- Rombos: Tienen los ángulos opuestos iguales, pero no necesariamente ángulos rectos.
- Romboides: Tienen los lados y ángulos opuestos iguales, pero no necesariamente ángulos rectos.
| Lados | Diagonales | Ángulos | Figura | |
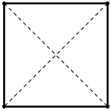
| Cuadrados | Todos los lados iguales y paralelos dos a dos. | Iguales que se cortan perpendicularmente en su punto medio. | Todos rectos. |
|
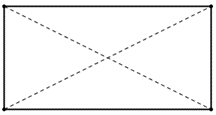
| Rectángulos | Lados opuestos iguales y paralelos dos a dos. | Iguales que se cortan en su punto medio. | Todos rectos. |
|
| Lados | Diagonales | Ángulos | Figura | |
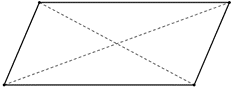
| Rombos | Todos los lados iguales y paralelos dos a dos. | No necesariamente iguales que se cortan perpendicularmente en su punto medio. | Opuestos iguales. | 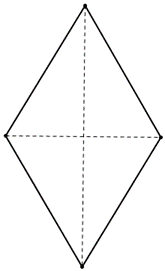 |
| Romboides | Lados opuestos iguales y paralelos dos a dos. | No necesariamente iguales que se cortan en su punto medio. |
Opuestos iguales. |
|
| Lados | Diagonales | Ángulos | Figura | |
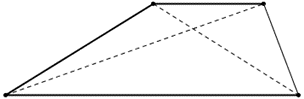
| Trapecios | Dos lados paralelos. |
|
||
| Trapezoides | Ningún par de lados paralelos. |
|
1. Cómo presentar la actividad al alumnado.
El recurso sirve para mostrar al alumnado cómo se pueden describir los distintos tipos de cuadriláteros atendiendo a sus propiedades y características. Así, a través de los botones de control, puede elegir y construir cualquier tipo de cuadrilátero. Es importante destacar cómo una misma figura, por ejemplo el cuadrado puede ser a la vez rombo y rectángulo. De esta posibilidad surge la necesidad de realizar una definición que satisfaga exclusivamente las características y propiedades de cada tipo de cuadrilátero. Para ello, se pueden presentar figuras que cumplan algunas y no todas las características según sus lados, diagonales y ángulos.
2. Indicaciones para interactuar con el applet.
El recurso propicia de una forma ágil y rápida la construcción de cualquier tipo de cuadrilátero según se indica en el propio menú. Posibilita la no fijación típica de la figura con los lados paralelos a los márgenes de la ventana. Integra la propia construcción la comprobación de las características del tipo de cuadrilátero dado.
3. Plantear actividades concretas sobre el tema que se aborda.
Una vez que el alumnado haya construido los distintos tipos de cuadriláteros podemos realizar actividades del tipo siguiente:
1.- Verifica con GeoGebra las siguientes afirmaciones:
- Una figura ABCD es paralelogramo ⇔ AB = CD y BC = AD.
- Una figura ABCD es un paralelogramo ⇔ BD ∩ AC = E, E punto medio de BD y E punto medio de AC.
- Las diagonales de un rombo son mediatrices.
Con ayuda de tu profesor puedes probar las anteriores proposiciones.
2.- Análisis de la figura que te presentamos en GeoGebra. Elige aquellas opciones correctas para cada una de los siguientes cuadriláteros:
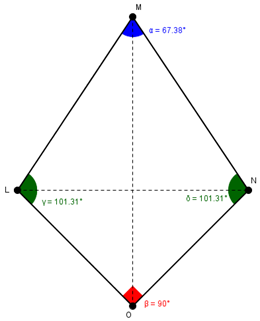 |
|
|
|
|
3.- ¿Sabrías cómo determinar el área de un paralelogramo? ¿Y el de un rombo?
4.- Realiza con GeoGebra la construcción siguiente. Con los datos que te mostramos podrías determinar el área de los cuadriláteros ABCD y STUV.
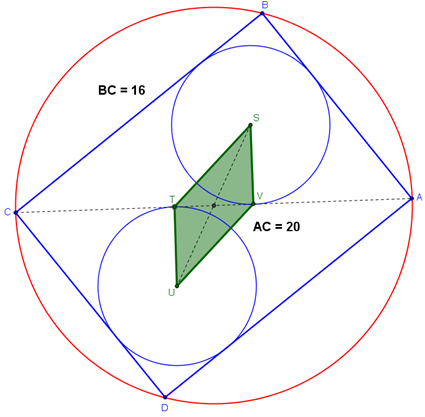
5.- Visualiza con GeoGebra el siguiente resultado geométrico: Uniendo los puntos medios de cualquier cuadrilátero podemos formar un paralelogramo (este resultado se denomina Teorema de Varignon).