Conocimientos previos
Fracciones, potencias y raíces
Nivel requerido al alumnado
Bajo
Interacción
Individual - Todo el grupo
Características del applet
Tipo de applet
Consolidar destrezas
Autocorregible
SI
Incluye preguntas
NO
Recomendaciones para su uso en el aula
Exposición por parte del profesorado - Trabajo individual - Trabajo para casa - Actividades de evaluación
Propuestas para su uso en el aula
Antes de empezar a usar el applet hay que comentar al alumnado que se va a abordar la forma de escribir un radical de cualquier índice y con exponente en el radicando en forma de una potencia con exponente fraccionario.
Es conveniente iniciar la sesión repasando los conceptos de radicales y exponentes viendo que los radicales son una forma de representar las raíces de un número, mientras que los exponentes se utilizan para representar la multiplicación repetida de un número por sí mismo. Y a continuación pasar a escribir los radicales en forma de exponente fraccionario haciendo hincapié en que esa forma de escribir no representa una multiplicación repetida.
Al acceder al applet aparecen 6 radicales que hay que expresar en forma de exponente fraccionario; para ello se debe introducir en la casilla de mayor tamaño la base del radicando y en las casillas de menor tamaño se deben introducir el exponente del radicando en la de arriba (que indicaría el numerador) y el índice del radical en la abajo (que indicaría el denominador).
Una vez colocados los tres números anteriores se puede pulsar en Clic para registrar aciertos (o pulsar en cualquier parte de la ventana o seguir con otro radical) y si la respuesta es correcta aparecerá una imagen con un clic o marca de verificación; si la respuesta no es correcta no aparecerá nada y se puede reintentar.
Después de los seis primeros intentos, al pulsar en el botón REINICIAR aparecerán otros 6 radicales para seguir practicando. Se puede pulsar tantas veces como se desee ya que el applet usa una cadena de números aleatorios para genera los índices y los radicandos.
Si se necesita volver al principio para seguir repasando se deberá pulsar en el botón arriba a la derecha de reinicio.
Actividades recomendadas:
1.- Una vez que se hayan expresados los radicales que aparecen en cada pantalla del applet en forma de potencia de exponente fraccionario, simplifica, si se puede, las fracciones de dichos exponentes y si el resultado es un número entero halla el resultado final del radical.
Ejemplos:
a) 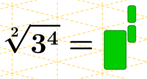 |
\(\sqrt[2]{3^4}=3^\frac{4}{2}=3^2=9\) |
b)  |
\(\sqrt[2]{8^6}=8^\frac{6}{2}=8^3=512\) |
c)  |
\(\sqrt[8]{7^6}=7^\frac{6}{8}=7^\frac{3}{4}\) |
2.- Usando las propiedades de las operaciones con potencias y después de haber practicado con el applet, expresa en forma de potencia de exponente fraccionario los radicales que aparecen en los siguientes ejercicios, opera con las potencias y simplifica al máximo volviendo a expresar en forma de un único radical.
| a) \(\sqrt[8]{\sqrt2}\) | b) \(\sqrt[5]{\sqrt3}\) | c) \(\sqrt[5]{x} ·\ \sqrt[5]{x^2}\) | d) \(\sqrt[4]{3} ·\ \sqrt[4]{27}\) | e) \(\sqrt[4]{2} ·\ \sqrt[4]{32}\) |
Ejemplo de solución:
e) \(\sqrt[4]{2} ·\ \sqrt[4]{32}=2^\frac{1}{4}\ · 2^\frac{5}{4}=2^{\frac{1}{4}+\frac{5}{4}}=\ 2^\frac{6}{4}=2^\frac{3}{2}=\sqrt[2]{3^3}\)