Conocimientos previos
Geometría elemental del triángulo.
Nivel requerido al alumnado
Cualquiera
Interacción
Individual
Características del applet
Tipo de applet
Introducir conceptos
Autocorregible
NO
Incluye preguntas
NO
Recomendaciones para su uso en el aula
Exposición por parte del profesorado - Trabajo individual
Propuestas para su uso en el aula
Presentación
El applet permite comparar los valores de las razones trigonométricas de un ángulo con los que se obtienen dividiendo las longitudes de los lados del triángulo rectángulo definido a partir de ese ángulo. Además, se pueden comparar los valores de las razones con los de la tabla para determinados ángulos. Por último, se puede comprobar cómo el tamaño del triángulo no influye en las razones trigonométrica.
Funcionamiento del applet
El applet tiene varios elementos que se pueden modificar, por un lado, el ángulo con un deslizador, pudiendo definir el ángulo desde 0° hasta 89,9999°
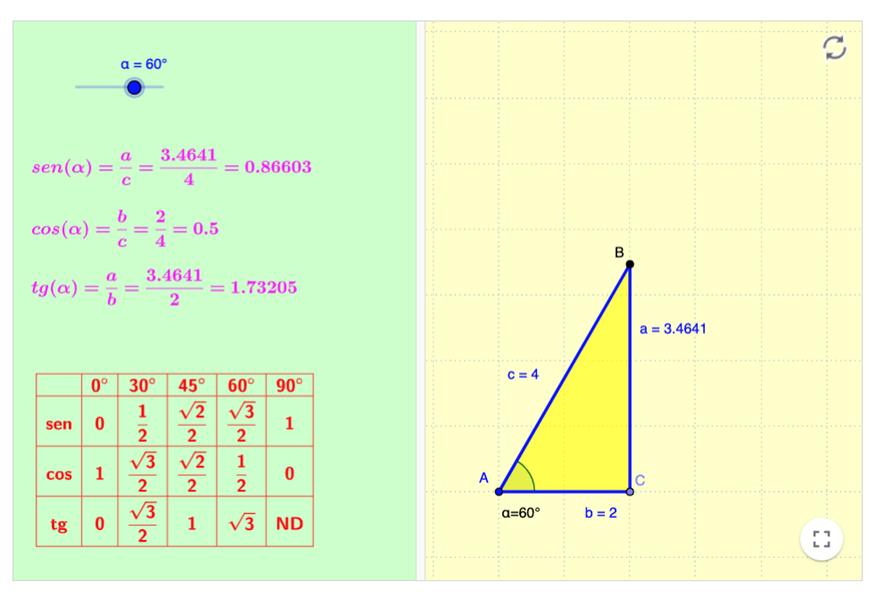
El triángulo rectángulo lo podemos variar de posición y tamaño, desplazando los puntos A y C (B está definido a partir de los otros dos y no se pueden desplazar)
A define el ángulo del que hallaremos las razones trigonométricas, a es el cateto opuesto, b es el cateto contiguo y c la hipotenusa.
A partir de la selección de los valores se calculan las razones trigonométricas aplicando la definición:
\(sen(α)=\frac{a}{c}, cos(α)\frac{b}{c}\enspace y\enspace tan(α)=\frac{a}{b}\)
La tabla muestra la definición de las razones trigonométricas de los ángulos mas usuales, es decir, 0°, 30°, 45°, 60° y 90° calculadas de formas exacta aplicando el teorema de Pitágoras, simplificando y racionalizando.
Ejemplos de ejercicios:
Ejercicio 1
Desplazamos los puntos hasta una posición en la que b=4 y α=30°
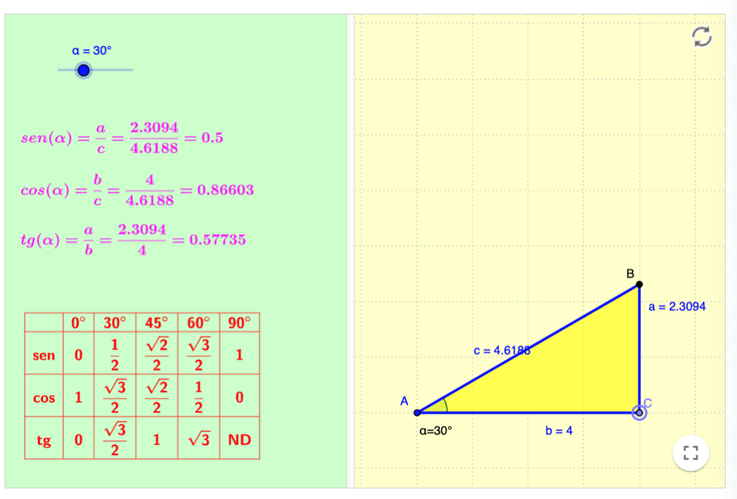
Usar la calculadora para comprobar el valor de las razones trigonométricas y compararlas con las que nos da el applet.
Después variar el tamaño del triángulo sin cambiar el ángulo y repetir el proceso
¿Cambian los valores cuando cambiamos el tamaño de triángulo?
Ejercicio 2
Repetir el ejercicio con b=4 y α=45° y después con b=3, además aplicar Pitágoras para comprobar el valor de la hipotenusa
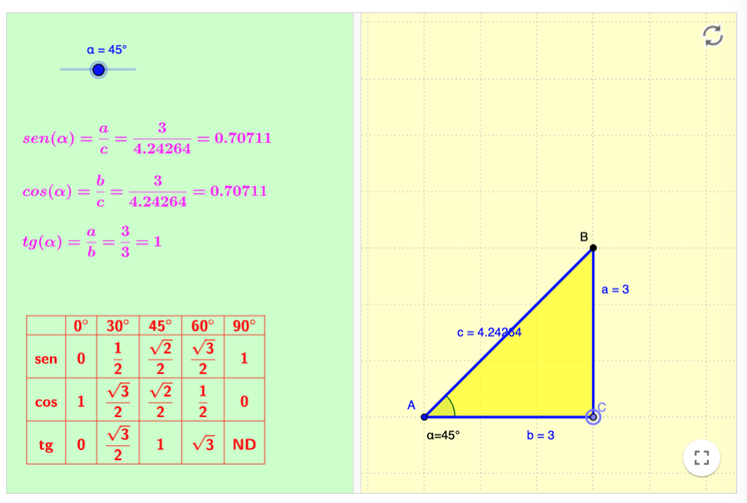
Ejercicio 3
Ahora queremos hallar las razones trigonométricas de 90°, pero no podemos visualizar el triángulo, para ello realizaremos una aproximación:
Calcula el ángulo más grande que puedas construir y que se visualice en pantalla, con el ratón “aléjate” hasta que visualices más y puedas aumentar el ángulo y seguir visualizando el triángulo completo. Repite varias veces y ve comprobando a que tiende cada una de las razones trigonométricas