1.1. La proporcionalidad hecha función.
 |
|
Frutas. Imagen de ppmuñoz en Flickr.
Licencia Creative Commons by-nc-sa |
La situación que has visto en el apartado anterior con las piezas de pan es muy corriente. Por ejemplo, si en una frutería vemos el kilogramo de kiwis a 1,20, es muy fácil calcular cuánto vale cualquier otra cantidad; ya que el medio kilo valdrá 60 céntimos de euro y kilo y cuarto nos costará 1,50 euros. Es decir, basta multiplicar la cantidad de kilogramos que compremos por el precio del kilo y obtenemos el valor de nuestra compra.
Dos magnitudes que se relacionan de esa forma (es decir, que una siempre se obtiene multiplicando la otra por un valor constante) reciben el nombre de magnitudes directamente proporcionales. Recuerda que dos magnitudes tienen una proporcionalidad directa, cuando al variar una de ellas, la otra varía en la misma proporción. Es decir, si una se duplica, la otra también; si una se reduce a la tercera parte, la otra se reduce en la misma proporción. En las magnitudes directamente proporcionales; tenemos la peculiaridad de que, si dividimos una entre otra, siempre se obtiene un valor fijo que se llama constante de proporcionalidad.
En este apartado vamos a estudiar las funciones que relacionan sus variables de esta misma forma.
Importante
Se llama función de proporcionalidad directa a toda aquella en la que la variable dependiente (y) se obtiene multiplicando la independiente (x) por un valor constante. Este tipo de función recibe más corrientemente el título de función lineal y tiene una expresión de la forma:
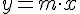
Toda función lineal tiene por gráfica una línea recta que pasa por el origen de coordenadas. Algo evidente; ya que, si en la expresión anterior le diéramos a x, el valor 0, la y también valdría 0, por lo que siempre se obtiene el par (0,0) como punto de la gráfica de este tipo de funciones.
Al valor m se le suele llamar pendiente de la recta y representa la inclinación de la recta respecto al eje de abscisas.
En la red
 |
En la venta interactiva, a la que accedes desde el siguiente enlace, puedes encontrar ejemplos resueltos de funciones que son lineales y de otras que se parecen pero no lo son. Mira los ejemplos que aparecen y copia en tu cuaderno las situaciones cotidianas en que aparecen funciones lineales. |
 |
|
Migas. Imagen de ppmuñoz en Flickr.
Licencia Creative Commons by-nc-sa. |
¿Comida y funciones?
Hace unas semanas estuvimos en un cortijo en el campo y para comer se prepararon migas. Para ello se necesitaron bastantes cosas, ya que aparte de los condimentos y material en sí, como agua, sal, pan, chorizos, pancetas, etc.. hubo varias personas preparando la comida, con un perol bastante grande y un buen fuego.
Queremos que nos indiques varias funciones que relacionen esos elementos con el número de comensales. Por ejemplo, la cantidad de pan, el número de platos necesarios, la cantidad de tiempo que se tarda en fregar todo lo ensuciado, el radio del perol según la cantidad de personas que van a comer, etc.
Describe al menos cuatro de esas relaciones e indica en cuál de ellas se trata de una relación funcional lineal y en cuáles no.
En la siguiente escena puedes ver una función lineal.
Si mueves el deslizador m representarás otra función lineal con distinta pendiente
Si mueves el punto P por la recta observarás que se verifica que el cociente entre la ordenada del punto y la abscisa es siempre el valor de la pendiente de la función lineal.
En particular, puedes observar que la pendiente es el valor que aumenta la y cuando la x aumenta una unidad.
Utiliza la ventana para poder contestar a la siguiente cuestión.
Función lineal. Applet de José Muñoz Santonja.
Licencia Creative Commons by-nc-sa.
| pendiente m mayor que cero |
|
pendiente m menor que cero |
En la red
 |
Tal como has visto en el applet de Geogebra que has manipulado antes, la pendiente en una función lineal es muy fácil de calcular. Basta tomar cualquier punto de la recta y dividir su segunda componente entre la primera. Como son variables directamente proporcionales, este cociente da siempre un valor fijo que es el valor de la pendiente.
Para practicar, puedes acceder a los ejercicios resueltos que aparecen en la página a la que te lleva el siguiente enlace. Practica con ellos y copia en tu cuaderno cuatro ejemplos de los que aparecen, dos de función creciente y otros dos decrecientes.
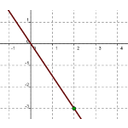
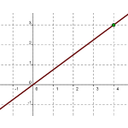
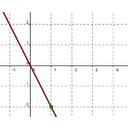
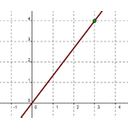
En la siguiente galería de imágenes tienes la gráfica de cuatro funciones lineales cuyas ecuaciones son las siguientes:
a) 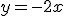 |
b) 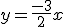 |
c) 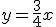 |
d) 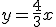 |
Coloca en cada casilla la letra que corresponde a la gráfica.
| Grafica 1:
|
Gráfica 2:
|
Gráfica 3:
|
Gráfica 4:
|
 |
|
Autobús. Imagen de ppmuñoz en Flickr.
Licencia Creative Commons by-nc-sa |
¿Cuánto nos cuesta el autobús?
Como hemos comentado desde el principio del tema, las funciones lineales son relaciones muy corrientes en nuestra vida cotidiana. Queremos que investigues un caso en el que aparece la relación entre, el número de viajes que realizamos en autobús urbano al mes y el coste que nos suponen esos desplazamientos.
Para ello, debes enterarte de cuál es el valor del viaje en el autobús urbano de tu ciudad o lugar de referencia. Después tendrás que construir la función lineal que relaciona el número de viajes con el coste total por esos desplazamientos.
Escribe en tu cuaderno la expresión de esa función lineal, construye una tabla de valores y dibuja la gráfica que corresponde a esa función.
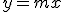 se verifica que si m>0 entonces la función es creciente y si m<0 entonces es decreciente.
se verifica que si m>0 entonces la función es creciente y si m<0 entonces es decreciente.