3.1. De un solo trazo.
 |
|
Entrada de un cine. Imagen del ITE en Banco de Imágenes del ITE.
Licencia Creative Commons by-nc-sa |
Hay ocasiones en que los valores que pueden tomar la variable independiente que estemos trabajando son aislados. Por ejemplo, si estudiamos la relación que hay entre el número de personas que están en una sala de cine viendo una película y la recaudación de las entradas, está claro que el número de personas puede ser 26 o 27, pero entre esos dos valores no hay valores intermedios posibles. Cuando a la variable independiente le ocurre esto decimos que es discreta.
Por el contrario, si nos fijamos en los pesos que tienen los pollos en un supermercado relacionándolos con su precio, es evidente que entre pesar 3 o 4 kilos hay muchos otros resultados posibles, por lo tanto, la variable independiente toma muchos valores intermedios y recibe el nombre de continua.
| Situación |
Tipo de variable |
| La relación entre la distancia recorrida por un vehículo y la gasolina consumida. | |
| La relación entre el número de viajes que realiza un camión y la cantidad de mercancía trasladada. |
|
| La relación entre el día del mes y la temperatura máxima alcanzada en una determinada ciudad. |
|
| La relación entre la cantidad de cerezas a granel (no empaquetadas) que compramos y su precio. |
|
Importante
Las funciones también pueden variar tomando todos los puntos intermedios o a saltos. Por ejemplo; si estudiamos la evolución del nivel de aguas de un pantano, es evidente que la cantidad de agua pasa por todos sus estados; es decir, no puede pasar de 100 hm3 a 99 hm3 sin pasar por los valores intermedios. Cuando ocurre esto, se dice que la función es continua. Suele decirse también que una función es continua, cuando su gráfica puede dibujarse de un solo trazo.
La función es discontinua en dos casos: cuando hay trozos de la variable dependiente que no se pueden obtener por la función o cuando o al dibujar la gráfica debemos levantar nuestro instrumento de dibujo para seguir dibujándola.
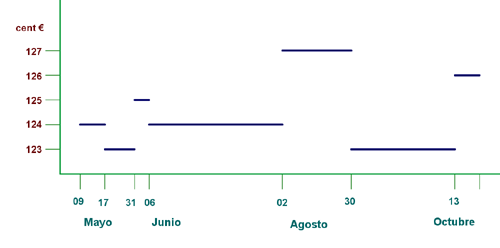
En la gráfica puedes ver un ejemplo de función discontinua. Tienes la evolución del precio del gasóleo A durante unos meses del año 2011. Cuando cambia el precio del gasóleo lo hace bruscamente, es decir, no cambia necesariamente céntimo a céntimo.
 |
Vamos a considerar tres situaciones cotidianas.
a) La evolución del precio de franqueo de una carta (valor del sello) en función del peso.
b) Evolución del gasto energético a lo largo de un día laborable en una gran ciudad.
c) Número de espectadores de un cine en los doce meses de un año.
Estas situaciones corresponden a funciones en las que hay las siguientes posibilidades:
- Variable independiente discreta.
- Variable independiente continua y función discontinua.
- Variable independiente continua y función continua.
Y debe corresponderle una de las siguientes gráficas:
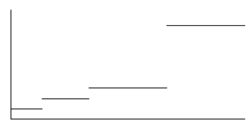 |
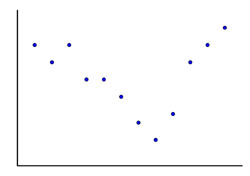 |
| f |
g |
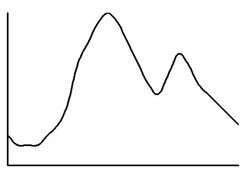
|
|
h |
Completa las huecos en blanco:
| Situación |
Función |
Gráfica |
| a |
||
| b |
||
| c |
¿Buscamos gráficas?
En los medios de comunicación es muy corriente que aparezcan gráficas lineales que no están bien dibujadas. Por ejemplo, es usual que se unan, mediante líneas, puntos que corresponden a variables discretas, es decir, que entre los dos valores que se presentan no hay valores intermedios. También es corriente que los ejes no estén correctamente divididos (no todas las divisiones son proporcionales) o se unan trozos verticalmente, no lo que no representa una función.
En esta tarea te vamos a pedir que busques dos gráficas de los medios de comunicación, una bien construida y la otra no. Debes escanear las imágenes y colocarlas en una entrada en el blog de aula indicando de qué medio las has tomado, que tipo de variable y función es (discreta, continua o discontinua) y qué error has localizado en la que no es correcta.