1.2. Ayudados por un árbol
Ya has visto cómo se realizan algunos recuentos directos. Ahora vamos a aprender a hacer recuentos en casos más complicados. Son aquellos recuentos en los que debemos aplicar herramientas matemáticas y un proceso previo antes de indicar la cantidad final de elementos que existen.
Para hacer estos recuentos indirectos vamos a utilizar un diagrama de árbol que nos ayude en el proceso. Veamos un ejemplo.
 |
|
Euro. Imagen del ITE en el banco de imágenes del ITE.Licencia Creative Commons by-nc-sa
|
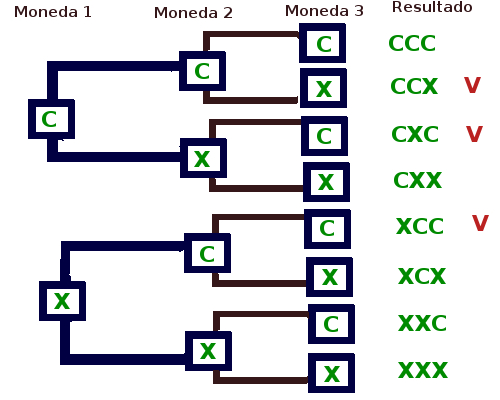
En esta ocasión lanzaremos tres monedas al aire y calcularemos cuántas formas posibles existen de obtener dos caras y una cruz. Atrévete a hacer el cálculo antes de ver la solución.
 |
| Construcción. Imagen de Juan Antonio Carabaña Aguado en el banco de imágenes del ITE.Licencia Creative Commons by-nc-sa |
Trifú
Ahora te toca practicar a ti. Para ello te vamos a proponer el siguiente experimento ficticio.
Imagina que tenemos un dado que vamos a llamar Trifú, en el que en cada una de sus caras aparece la imagen de una de las siete maravillas del mundo (actuales), excepto la que observas en la imagen de la derecha. El experimento consiste en que lances un dado normal. Si el resultado del lanzamiento es un número par, lanzas una moneda y si el resultado del lanzamiento es un número impar, lanzas el dado Trifú. Dibuja un árbol en tu libreta en el que se observen los posibles resultados de este experimento y señala aquellos en los que aparezca una cara.
Realiza una fotografía del esquema que has creado. Realiza una entrada en el blog de aula en la que cuentes las dificultades que has encontrado a la hora de resolver la tarea e incrusta en ella ti imagen. La entrada deberá tener dos etiquetas. La primera será la primera letra de tu nombre seguida de tu primer apellido y la segunda será el nombre del país en el que se encuentra la construcción que observas en la imagen.
En la red
 |
| Escarabajo. Imagen del ITE en el banco de imágenes del ITE.Licencia Creative Commons by-nc-sa |
En el cuento de Edgar Allan Poe "El escarabajo de oro" el protagonista (el señor Legrand) encuentra un tesoro gracias a que es capaz de descifrar un texto en clave con las pistas suficientes para ir en su busca.
El señor Legrand consigue descifrar el texto cifrado porque va sustituyendo cada signo (cifra o símbolo) por una letra del abecedario; teniendo en cuenta que los signos que más se repiten deben corresponder, más o menos, a las letras que más se usan en español: la E, la A, la O...
 |
En el siguiente enlace
encontrarás una actividad en la que deberás utilizar tus dotes
científicas para contar y resolver el enigma. Después del mensaje en clave puedes ver, en rojo, el abecedario ordenado por orden de frecuencia: la letra más usada es la E, seguida de la A, etc.
Anota en tu cuaderno
la solución y comparte con tus compañeros las deducciones que has
realizado para resolverlo.
|
Curiosidad
A veces puede resultar muy complicado realizar un recuento tanto directa como indirectamente. En estas ocasiones se suele hacer uso de técnicas estadísticas para llegar a una aproximación del número de unidades existentes. Estos procedimientos son muy fiables, ya que el error está controlado por técnicas matemáticas.
Por ejemplo, imagina que debes calcular el número de peces que hay en un estanque grande. Para contarlos, si el número es grande, deberíamos ir pasando los peces uno a uno a otro estanque. Pero una solución es la que te ofrecemos en la siguiente ventana interactiva.
|
|
|
Peces de un estanque. Animación de Jorge Sánchez en el banco de imágenes del ITE.
Licencia Creative Commons by-nc-sa |
La cifra final que se indica no es una cantidad exacta, sino una cifra aproximada del número de peces que hay en el estanque. Esta misma técnica se utiliza para calcular el número de ejemplares de peces que puede haber en un pantano o el número de aves de una especie que puede haber en un bosque.