2.3. Cálculo de probabilidades sencillas
Comprueba lo aprendido
|
|
|
Probabilidad de la unión de sucesos. Animación de Isabel Martín Rojo en banco de imágenes del ITE
Licencia Creative Commons by-nc-sa |
En la animación de la derecha puedes observar la forma de calcular la probabilidad de la unión de dos sucesos en un determinado experimento aleatorio. Te vamos a pedir que investigues a fondo sobre la probabilidad y que indiques qué afirmaciones de las que aparecen más abajo son verdaderas y cuales son falsas. Partimos de dos experimentos independientes E1 y E2. En el primer experimento (E1) vamos a considerar dos sucesos A y B. En el segundo experimento (E2) vamos a considerar un suceso C.
Una vez que hayas investigado y localizado las afirmaciones que son ciertas, anótalas en tu cuaderno. Posteriormente, deberás buscar ejemplos de dos experimentos, E1 y E2, y seleccionar dos sucesos del primer experimento y un suceso del segundo.
Con los resultados de este trabajo deberás realizar una presentación con Impress en la que se observe que se cumplen las propiedades que eran verdaderas y no se cumplen aquellas que eran falsas. Utiliza esta presentación en clase para exponer al profesor y a tus compañeros y compañeras los frutos de tu investigación.
Responde a las siguientes preguntas:
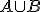significa que ocurra el suceso A o que ocurra el suceso B, se tiene que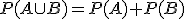 
significa que ocurra A o que ocurra B, se tiene que 
Tarea
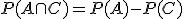
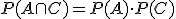
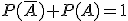
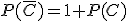
Ya has usado para una tarea anterior la baraja española de cartas. En esta te vamos a pedir dos cosas relacionadas con dicha baraja. La primera es que resuelvas el problema que te planteamos en el siguiente vídeo:
|
|
|
La baraja española de cartas. Vídeo de mariano31415 en Youtube
Licencia Creative Commons by-nc-sa |
La segunda es que inventes y resuelvas un ejercicio parecido al que se plantea en el vídeo y que esté relacionado con la baraja española.
Lleva a cabo una exposición oral de la resolución del ejercicio del vídeo y el enunciado y resolución del ejercicio que has planteado.
Tarea
¿Conoces la baraja francesa? Si no es así, sería conveniente que investigaras sobre ella ya que la siguiente tarea está relacionada con este tipo de cartas. En este caso, en el vídeo siguiente te pedimos que calcules una probabilidad usando los naipes de esta baraja.
|
|
|
La baraja francesa de cartas. Vídeo de mariano31415 en Youtube
Licencia Creative Commons by-nc-sa |
Realiza los cálculos necesarios, anótalos en tu cuaderno y compártelos posteriormente con tus compañeros.
Tarea
 |
|
Cama. Imagen del ITE en banco de imágenes del ITE
Licencia Creative Commons by-nc-sa |
¿Te han hecho una encuesta alguna vez en casa? Seguramente la respuesta sea no. Por eso, te habrás preguntado de dónde salen las estadísticas que nos muestran en los medios de comunicación. La verdad es que es bastante complicado que seas entrevistado para una de estas encuestas. ¿Por qué? Intentaremos explicarlo a través de esta tarea.
Imagina que van a realizar un estudio sobre la altura de las personas para que los fabricantes de camas ajusten las medidas de las mismas al tamaño real de la población. Vamos a formularnos varias preguntas acerca de esta hipotética encuesta.
Lo primero que debes conocer es que cuando se realizan encuestas en casa, previamente se ha realizado un sorteo para conocer las casas en las que se va a realizar la encuesta. Esto se conoce como muestreo.Supongamos que en la provincia en la que vives se ha realizado un sorteo entre los distintos pueblos que la componen, para hacer una encuesta. ¿Qué probabilidad hay de que haya salido seleccionada tu localidad?
Si dentro de tu localidad, ha salido agraciada la calle en la que vives, ¿Qué probabilidad hay de que sea seleccionado el portal o vivienda en la que vives?
Si dentro de tu vivienda se realiza un sorteo entre las personas que habitáis en ella, ¿qué probabilidad hay de que la encuesta te la hagan a ti?
Realiza un vídeo utilizando en el que expliques las respuestas a las anteriores preguntas y justifiques cada una de esas respuestas. En el vídeo deberás indicar además si crees que es fácil que seas elegido para una encuesta y por qué. Sube el vídeo a Internet y realiza una entrada en el blog de aula en la que cuentes las dificultades que has encontrado a la hora de resolver la tarea. Incrusta en la entrada tu vídeo. La entrada deberá tener dos etiquetas. La primera será la primera letra de tu nombre seguida de tu primer apellido (por ejemplo, de Mariano Real será mreal) y la segunda será el nombre de tu localidad.
Curiosidad
 |
|
Niña romana jugando a las tabas. Imagen de wikimedia en Wikipedia
Licencia Creative Commons by-nc-sa |
¿Desde cuando se juega a los dados?
En la Edad de Piedra, los hombres ya jugaban, como se hace hoy en día con los dados, con unos huesecillos llamados tabas o astrágalos . Con la taba de algunos animales, particularmente del cordero, se practica un juego de apuestas muy simple, el juego de las tabas, conocidas más recientemente como gogos. El juego consiste en lanzar la taba y apostar acerca de dónde y cómo quedarían las partes salientes del hueso.
Si estas partes quedan hacia arriba, se gana una o cuatro unidades apostadas mientras que si quedan hundidas, se pierden una o cuatro unidades apostadas. Actualmente, también se fabrican imitaciones del hueso de plástico para el juego, además de variaciones de figuras de distintas formas y colores. También existen otras con 4 caras de formas diferentes para versiones infantiles del juego.
También se encontraron restos de dados cúbicos en tumbas de Egipto de hace más de 4000 años. Se dice que los soldados griegos ya jugaban hace 3000 años durante la guerra de Troya. También los romanos usaban dos tipos de dados: unos cúbicos llamados tessere y otros en forma de prisma rectangular llamados talí.
