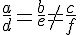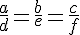2.2. Disparidad en el número de soluciones.
En nuestra vida cotidiana, hay muchos certámenes en los que el resultado puede variar según las candidaturas presentadas cada año. Se puede declarar desierto si la calidad no es muy buena en opinión del jurado, entregarse a una persona o institución o entregar el premio a varios candidatos distintos de forma ex aequo. Un par de estas posibilidades puedes observarlas en el recorte de prensa que te adjuntamos.
|
Divulgación Fernando Corbalán, premio José Mª Savirón La última edición del Premio José María Savirón de Divulgación Científica ya tiene ganadores. En su categoría aragonesa, el jurado ha decidido reconocer la continuada labor divulgativa desarrollada por el matemático Fernándo Corbalán. En su dilatada trayectoria, ha mostrado a todo tipo de públicos las matemáticas presentes en la vida cotidiana, a través de exposiciones, artículos y libros, así como desde el programa educativo Matemática Vital. Es colaborador de Heraldo Escolar desde 1985, y precisamente la semana pasada presentó en Zaragoza su libro "Mates de cerca" (editorial Graó), que recoge los artículos publicados en dicho suplemento. En la categoría nacional, el galardón ha recaído ex aequo en Jorge Mira Pérez, de la Universidad de Santiago de Compostela, organizador de Con-Ciencia, iniciativa en la que han participado varios premios Nobel; y en el programa de divulgación científica de la 2 de Televisión Española "Tres 14", que dirige Ana Montserrat Rosell. |
| Noticia del Heraldo.com. |
Algo parecido pasa con las ecuaciones. Ya viste, en la unidad anterior, que las ecuaciones de segundo grado podían tener 0, 1 o 2 soluciones según los coeficientes de la ecuación. En los sistemas va a pasar algo parecido.
Importante
Según el número de soluciones, los sistemas de ecuaciones lineales se pueden clasificar de la siguiente forma:
- Sistema Compatible Determinado: tiene una única solución.
- Sistema Compatible Indeterminado: tiene infinitas soluciones. Basta que tenga dos soluciones distintas para que sean solución todos los valores que satisfacen a una cualquiera de las dos ecuaciones.
- Sistema Incompatible: no tienen solución.
 |
Gráficamente es muy fácil saber en qué tipo de sistema estamos. Como viste en el apartado anterior, la representación gráfica de una ecuación lineal con dos incógnitas era una línea recta. Si tenemos un sistema; gráficamente tendremos dos líneas rectas y, según su posición, podremos saber cómo es el sistema.
- Si las dos rectas se cortan en un punto, el sistema es compatible determinado.
- Si las dos rectas coinciden, todos los puntos satisfacen a las dos ecuaciones y el sistema es compatible indeterminado.
- Si las dos rectas son paralelas, entonces no hay punto común y el sistema es incompatible.
|
Solución gráfica de un sistema. Applet creado por José Muñoz Santonja. Licencia Creative Commons by-nc-sa |
Utiliza el applet anterior para representar sistemas y, al mismo tiempo, estudiar cómo se tienen que comportar sus coeficientes para que el sistema sea de un tipo u otro. Después, resuelve en tu cuaderno la siguiente tarea:
Manipula la ventana para representar los siguientes sistemas. Debes decir qué tipo de sistema es cada uno y cuál es su solución (ten presente que cuando el sistema no tenga solución única aparece en pantalla que la solución del sistema es indefinida).
| a) |
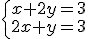 |
b) |
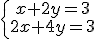 |
c) |
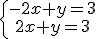 |
| d) |
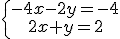 |
e) |
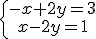 |
f) |
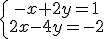 |
Una vez que hayas encontrado de qué tipo es cada sistema, estudia la relación que debe haber entre los coeficientes de una ecuación y otra para que el sistema sea: compatible determinado o indeterminado, o bien incompatible.
En la red
 |
Para comprobar si has asimilado lo que hemos trabajado, realiza los tests que encontrarás en el siguiente enlace. Resuelve los 5 primeros tests que corresponden a "clasificación". Después, responde a los tests del 8 al 11. En estos últimos aparecen una serie de sistemas clasificados por tipo. Escribe en tu cuaderno tres ejemplos de cada tipo. |
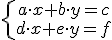 e indicar en cada caso cómo es el sistema.
e indicar en cada caso cómo es el sistema.
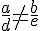 .
.