Operaciones con sucesos
Importante
El espacio muestral E y los sucesos pueden ser representados en diagramas de Venn, como puedes observar en la siguiente imagen.
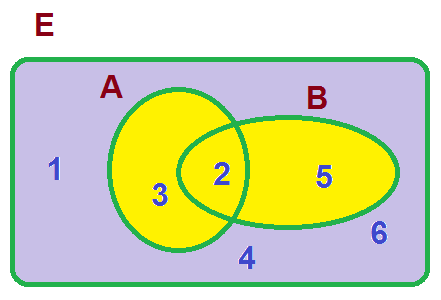
En la imagen se representa el espacio muestral E = {1,2,3,4,5,6}, correspondiente al experimento aleatorio de lanzar un dado con sus caras numeradas del 1 al 6. Las zonas amarillas se corresponden a los sucesos A = {2,3} y B = {2,5}.
Ejemplo o ejercicio resuelto
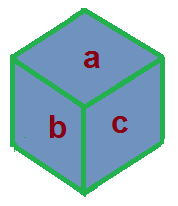
Supongamos que hemos grabado en cada cara de un dado las letras a,b,c,d,e y f. Representa en tu cuaderno, mediante diagramas de Venn, el espacio muestral relativo al experimento aleatorio consistente en lanzar dicho dado. El suceso A consiste en salir una vocal y el suceso B consiste en salir las consonantes comprendidas en el alfabeto entre la a y la e.
Fíjate en el ejemplo de la imagen anterior.
Importante
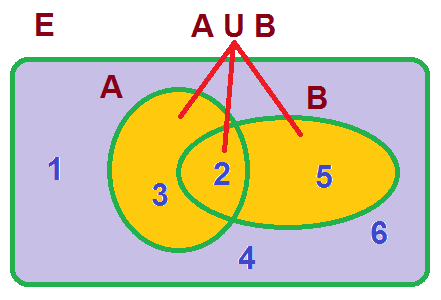
- La unión de dos sucesos A y B es el suceso formado por los de A y B. Se representa por A U B. Por ejemplo, dado el suceso A = {2,3} y el suceso B = {2,5}, la unión será A U B = {2, 3,5}.
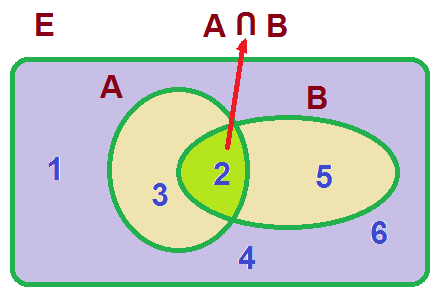
- La intersección de dos sucesos A y B es el suceso formado por los sucesos comunes de A y B. Se representa por A ∩ B . Por ejemplo, dado el suceso A = {2,3} y el suceso B = {2,5}, la intersección será A ∩ B = {2}.
Aprende a hacerlo
Consideremos el experimento aleatorio consistente en lanzar un dado con sus caras numeradas con los números 2,4,5,6,10 y 12. Sean los siguientes sucesos:
- A, consistente en salir un número primo.
- B, consistente en salir un número múltiplo de 3.
- C, consistente en salir un número múltiplo de 5.
Comprueba lo aprendido
En la red
En el siguiente enlace puedes realizar un repaso de los contenidos que hemos desarrollado sobre los experimentos aleatorios y las operaciones con sucesos.
Realiza las distintas actividades que se proponen en el apartado "sucesos de un experimento aleatorio. Tipología".
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0