1.2. Esto es recurrente.
A veces, las sucesiones se dan de forma recurrente. Por ejemplo, en la sucesión 8, 13, 18, 23, ... podemos ver que cada término se obtiene sumando 5 unidades al anterior. Podemos por tanto decir que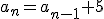 
. Pero, aún así, es fácil encontrar un término general, en concreto, 
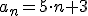. Sin embargo, hay otras sucesiones recurrentes en las que no es tan fácil encontrar el término general, por ejemplo, 1, 5, 14, 30, 55, 91, ... tiene como ley de recurrencia 
.
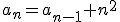Dentro de las sucesiones recurrentes la más conocida es la Sucesión de Fibonacci, que vimos en el vídeo de la introducción. En esa sucesión, 1, 1, 2, 3, 5, 8, 13, ... cada término, a partir del tercero, se calcula sumando los dos anteriores. Es decir, su ley de formación sería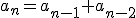 
. Aunque puede parecer que es una sucesión extraña vamos a ver que tiene muchas aplicaciones.
Tarea
En el siguiente enlace tienes el material interactivo del programa "Fibonacci: la magia de los números" de la serie Más por menos de RTVE.
En ella encontrarás una pequeña información sobre Leonardo de Pisa, más conocido como Fibonacci, y cosas muy interesantes sobre la sucesión que lleva su nombre. Especialmente, verás como es posible encontrar esta sucesión en la naturaleza.
Te recomendamos que realices las actividades interactivas que aparecen en las tres partes en las que se divide "Fibonacci: la magia de los números"
Además, la tarea que tendrás que realizar sobre los contenidos tratados en los diferentes vídeos tiene dos partes.
 |
En la primera parte de la tarea deberás contestar en tu cuaderno al cuestionario que encontrarás en el siguiente enlace.
La segunda parte de la tarea consistirá en que realices un informe de texto, por ejemplo en Google Docs en el que hables sobre Leonardo de Pisa y especialmente sobre su aportación a la historia de la matemática. Lo complementarás con una explicación sobre el número de oro y su aplicación en el arte y otros aspectos de la vida cotidiana.
El texto que realices debes compartirlo en la red e incrustarlo en el blog de aula añadiendo dos etiquetas: la típica de tu nombre y fibonacci como segunda etiqueta.
Tarea
 |
|
Magia matemática. Imagen de ppmuñoz en Flickr.
Licencia Creative Commons by-nc-sa |
¿Magia?
Hay varios trucos de magia matemática que se basan en una sucesión con la misma construcción que la de Fibonacci. Vamos a ver un par de ellos:
1. Se pide a un espectador que seleccione dos números cualesquiera de dos cifras. A continuación, debe crear una sucesión de forma que cada término sea la suma de los dos anteriores. En total debe escribir 20 términos. Por último, debe dividir el término 20 entre el 19. El mago ya tendrá un papel en la que figurará el número 1,61803... que son las primeras cifras del número de oro y que coincidirá con lo obtenido en la división.
Comprueba este truco. Para ello toma una hoja de cálculo y a partir de los dos primeros términos halla los 20 primeros de la sucesión y comprueba que realizando la división indicada, se obtienen las cifras anteriores. Indica en tu cuaderno los dos números de los que has partido inicialmente y a partir de qué término se obtiene la primera cifra decimal del número de oro, a partir de qué término se obtienen las dos primeras cifras decimales exactas, cuándo ocurre con las tres primeras y así hasta las 5 que hemos indicado.
2. El segundo truco consiste en la misma sucesión. Partimos de dos números cualesquiera, se le pide al espectador que comience a construir la sucesión hasta el término 10. Cuando el espectador haya escrito el 7º término el mago puede hacer ya una predicción del valor que se va a obtener al final, escribiéndolo en un cuaderno.
Una vez que se escriban los 10 términos se suman y el valor de la suma coincide con el número que había previsto el mago.
Lo que queremos que hagas es que utilices las expresiones algebraicas para estudiar que relación existe entre el valor de la suma y el 7º término de la sucesión. Escribe en tu cuaderno todo el proceso que has seguido y la explicación sobre el truco que utiliza el mago para hallar el valor.
