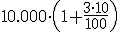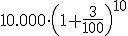4.1. Todo por el interés.
 |
|
Todo por el interés. Imagen de ppmuñoz en Flickr.
Licencia Creative Commons by-nc-sa
|
Una de las cosas más corrientes en nuestro mundo son las relaciones financieras con los bancos. Rara es la familia que no tiene algún tipo de cuenta en un banco, bien porque se tenga algún dinero invertido o algún plan de pensiones, o bien, como ocurre en muchos casos, porque se haya pedido un préstamo para adquirir una vivienda, algún vehículo o incluso afrontar un gasto extra como una boda o un viaje. Lo cierto es que prácticamente todo el mundo sabe lo que es un interés bancario y, casualmente, esos intereses tienen mucho que ver con las progresiones.
En general, cuando una cantidad monetaria cambia de manos mediante un préstamo o imposición, es necesario devolver la cantidad inicial mas otra cantidad que corresponde a los beneficios que quiere obtener el que presta el dinero. Esa cantidad se llama interés, y suele darse en tanto por ciento.
Hay dos tipos de interés: el que se recoge año a año, que recibe el nombre de interés simple, y otro que se va incorporando a la cantidad inicial y sólo se recoge al final (por lo que esa cantidad también incrementa, cada año, la cantidad inicial). Este segundo tipo recibe el nombre de interés compuesto.
Veamos un ejemplo numérico. Consideremos que ingresamos 12.000 euros en una entidad bancaria y nos dicen que nos van a dar un 4% de interés. Veamos cómo varía la cantidad que tenemos según el tipo de interés. Representamos por Ci el capital inicial que tenemos al principio del año y por Cf la cantidad final que tenemos en un determinado momento.
| Interés simple |
Interés compuesto |
|||||
| Año |
Ci |
Interés | Cf |
Ci |
Interés |
Cf |
| 1 |
12.000 |
480 |
12.480 |
12.000 |
480 |
12.480 |
| 2 |
12.000 |
480 |
12.960 | 12.480 |
499,20 |
12.979,20 |
| 3 |
12.000 |
480 |
13.440 | 12.979,20 |
519,17 |
13.498,37 |
| 4 |
12.000 |
480 | 13.920 |
13.498,37 |
539,93 |
14.038,30 |
Si representamos por r el tanto por ciento que nos ofrecen de interés, podemos apreciar que en el primer caso nos encontramos con una progresión aritmética cuya diferencia es 480, equivalente a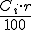 
. En el caso del interés compuesto, cada año se multiplica por 1,04 (ya que se haya el 4% de la cantidad inicial en ese año). Luego tenemos una progresión geométrica donde la razón es 
.
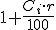Por eso, las fórmulas para los distintos intereses suponiendo que tenemos un capital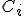 
invertido al r% durante t años son:
Comprueba lo aprendido
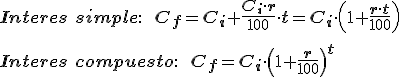
Indica la cantidad que tendremos después de los 10 años en los dos casos:
Interés simple: euros.
Interés compuesto: euros.
Atención: Utiliza el punto para las unidades de millar y escribe dos cifras decimales cuando la cantidad no sea entera.
En la siguiente ventana, tienes un estudio comparativo sobre lo que se consigue poniendo una cierta cantidad al 4%, según se haya colocado con interés simple (sin amortización) o compuesto (con amortización).
Puedes modificar el número de años que se tiene invertido para que compruebes que cuántos más años, mayor es la diferencia.
Término general (forma T). De Consolación Ruiz Gil en Descartes.
Licencia Creative Commons by-nc-sa.
Comprueba lo aprendido
Tarea
 |
|
Motos. Imagen de ppmuñoz en Flickr.
Licencia Creative Commons by-nc-sa |
¿Qué moto te gusta?
Vamos a suponer que deseas continuar tus estudios para hacer estudios superiores. Una vez que acabes la ESO y el Bachillerato, pensarás si estudiar en una Universidad o hacer un módulo superior de Formación Profesional.
Como en ambos casos es casi seguro que estudiarás lejos de casa, estás pensando en comprarte una moto cuando termines tus estudios en el instituto, para poder desplazarte con tranquilidad.
La tarea que te proponemos es la siguiente. Debes elegir qué modelo de moto te gustaría comprarte y localizar su precio. Vamos a suponer que, dentro de cuatro años, el precio es el mismo y que para, poder comprarla, vas a invertir en un banco dinero ahora mismo para que este te produzca la cantidad necesaria.
Debes, por tanto, buscar una entidad bancaria que te ofrezca el mejor interés y estudiar qué cantidad debes ingresar ahora mismo, a interés compuesto, para que cuando recuperes tu dinero dentro de cuatro años puedas pagar la moto.
Realiza una presentación en la que muestres todos los datos y cálculos que has utilizado: tipo de moto, precio, entidad bancaria seleccionada, tipo de interés, etc.
