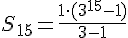3.3. La suma de una parte.
En la siguiente presentación puedes ver cómo se consigue la fórmula y un ejemplo de aplicación. Recuerda que basta con que pulses sobre la pantalla para pasar a la siguiente diapositiva.
|
|
|
Suma de progresión geométrica. Montaje de José Muñoz Santonja.
Licencia Creative Commons by-nc-sa
|
Consideramos la progresión geométrica formada por las potencias de 3, comenzando en la potencia de exponente cero, es decir, en 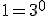 .
.
La suma de las 15 primeras potencias de 3 vale .
En la ventana tienes ejemplos resueltos de cálculo de la suma de n términos de una progresión geométrica.
Debes copiar en tu cuaderno cuatro ejercicios, uno de cada uno de los tipos diferentes que aparecen. Los tipos son: calcular la suma cuando se conoce el término general, un término y la razón, dos términos, o los primeros términos de la sucesión.
A medida que copies el enunciado debes resolver los ejercicios y, posteriormente, comprobar la solución en el applet. Si tienes algún error, repasa los cálculos; de forma que en el cuaderno quede la resolución correcta, aunque no siga el mismo proceso que en el applet.
Suma de progresión geométrica. De Miguel Ángel Cabezón Ochoa en EDAD.
Licencia Creative Commons by-nc-sa.
 |
|
Saque de puerta.Imagen de Antonio David Fernández en Flickr.
Licencia Creative Commons by-nc-nd |
Después de unas semanas de vacaciones, los profesionales del futbol comienzan a entrenar para preparar la nueva temporada. El entrenador ha encargado al portero que entrene los saques de puerta con el pie. En uno de los primeros intentos consigue que el balón se desplace 50 metros. Dado que no hay ningún jugador que lo frene y por las condiciones del césped y del balón después de botar, el balón sigue avanzando. No obstante, después de cada bote avanza, aproximadamente, dos quintas partes de los metros recorridos en el anterior bote.
- Calcula cuánto habrá avanzado después de cinco botes. ¿Y después de cinco botes más?
- ¿Alcanzará el balón la portería contraria en esos 10 botes?
- Si lo anterior no se consigue, encuentra cuánto debe desplazarse el balón en el primer salto para que llegue a la portería contraria.
Haz los mismos cálculos si suponemos que el portero es de fútbol sala. Ten presente que en este caso debe sacar con la mano, por lo que debes estimar cuánto puede desplazarse el balón en el primer desplazamiento.
Copia el enunciado en tu cuaderno y contesta a las cuestiones.
 |
|
Ciclista. Imagen del ITE en Banco de Imágenes del ITE.
Licencia Creative Commons by-nc-sa |
Dos ciclistas se están preparando para una competición. Fernando comienza entrenando 1000 m. el primer día y aumenta 1000 m. más por cada día de entrenamiento.
Manolo, por su parte, comienza corriendo 60 m. el primer día pero después, durante cada uno de los 10 días de entrenamiento, duplica la cantidad del día anterior.
Queremos saber cuántos metros corren cada uno el décimo día, y cuántos metros han entrenado en los diez días de preparación.
Escribe las cantidades con el punto para indicar las unidades de millar.
|
Metros el día 10º |
Metros totales en los 10 días |
|
| Fernando | ||
| Manolo |