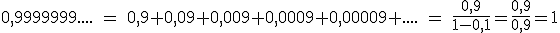3.4. Lo queremos todo.
Siempre que vamos sumando los términos de una progresión, el valor de la suma va aumentando; de forma positiva o negativa según el signo de los términos. En muchos casos, cuando se añade un número indeterminado de términos, la suma va haciéndose infinita, Pero ¿ocurre esto siempre?
La respuesta es no. Piensa en la tarea que has resuelto en el apartado anterior. Habrás comprobado que el balón, en los primeros cinco botes recorre una gran parte del campo, pero en los siguientes cinco avanza muy poco (y avanzará menos si sigue menguando la distancia recorrida en cada bote). En general, cuando tenemos una progresión geométrica en la que la razón es menor que la unidad, los términos de la progresión se van haciendo cada vez más pequeños. Veamos el siguiente ejemplo:
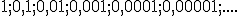
Es evidente que podemos considerar que a partir de un determinado momento los términos valen prácticamente cero.
Por ello, en las progresiones geométricas podemos hallar la suma de todos los términos de la progresión. Basta considerar en la fórmula que dedujimos en el apartado anterior que para un valor n suficientemente grande, an=0. De esa forma, la suma de los infinitos términos de una progresión geométrica de razón menor de la unidad viene dada por la fórmula:
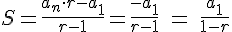
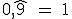
En la red
|
En el siguiente enlace puedes apreciar que la suma de infinitos términos de una progresión geométrica de razón 1/2 no es infinita, como podría pensarse, sino finita. Encontrarás un applet de Geogebra en el que podrás estudiar de forma geométrica la construcción de la progresión y el cálculo de su suma. Tras el applet hay una serie de cuestiones para contestar en tu cuaderno. |
 |
Curiosidad
 |
|
Zenon de Elea. Imagen de dominio público alojada en Wikipedia.
Licencia Wikimedia Commons |
El suponer que la suma de infinitos términos siempre da infinito es un pensamiento muy corriente desde la antigüedad.
En la antigua Grecia dio lugar a que algunos filósofos idearan razonamientos que intentaban comprobar que utilizando las reglas matemáticas, se llegaba a negar lo evidente. Es lo que se conoció como paradojas, en cuyo desarrollo fue un maestro Zenón.
El filósofo griego del siglo V a.C., Zenón de Elea, era discípulo de Parménides y se dedicó a atacar todo planteamiento que no siguiese la escuela filosófica a la que pertenecía. Por ello, elaboró una serie de razonamientos que han sido muy famosos a lo largo de muchísimos años.
Todos se basan en suponer que una suma de infinitos términos se hace tan grande como se quiera y que un proceso indefinido nunca tiene limitación, aunque los términos se vayan haciendo cada vez más pequeños.
En una de sus paradojas planteaba que si un arquero debía lanzar una flecha a una diana, antes de recorrer toda la distancia hasta la diana la flecha tendría que recorrer la mitad del espacio, y antes de eso la mitad de esa primera parte, y para ello primero debería surcar la mitad de la parte anterior, y antes la mitad de esa mitad.
Siguiendo así el razonamiento indefinidamente la conclusión era que la flecha no se movía.
 |
Pero quizás la paradoja más conocida sea la de Aquiles y la Tortuga que puedes conocer en el siguiente enlace.
Actividad de Lectura
 |
En el siguiente enlace puedes leer un párrafo del libro Matemáticas, ¿estás ahí? del profesor argentino Adrián Paenza, gran divulgador de la matemática a través de sus libros y sus apariciones en televisión de las que existen muchos ejemplos en YouTube. |
El apartado que queremos que leas lleva por título "¿Cuántas veces se puede doblar un papel?". Una vez que leas esa obra , debes hacer un resumen de entre 5 y 10 líneas en el que expliques las ideas fundamentales que se desarrollan. Piensa que le estás contando a un amigo lo que has leído y quieres indicarle lo más importante.
Además, debes contestar a las siguientes cuestiones:
Si suponemos que el papel que se utiliza para doblar es lo suficientemente grande para conseguirlo,
- ¿Cuántas veces deberíamos doblarlo para alcanzar la distancia de la Tierra a la Luna?
- ¿Y la distancia de la Tierra al Sol?
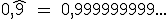 puede considerarse como la suma de los términos de una progresión geométrica cuyo primer término es 0,9 y la razón 0,1:
puede considerarse como la suma de los términos de una progresión geométrica cuyo primer término es 0,9 y la razón 0,1: