Debemos seguir, generalmente, el siguiente proceso recomendado por expertos en didáctica de las Matemáticas:
Además, estas fases debemos aplicarlas y complementarlas con el trabajo en equipo, fundamental para conseguir el éxito.
Por si fuera necesario, ofrecemos aquí algunas pautas concretas con la intención de ayudar en la resolución de cada uno de los problemas y que podamos elaborar el informe técnico correspondiente con la mayor calidad posible.
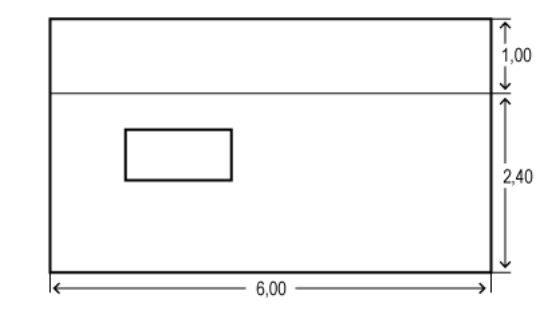
El patio
1.- ¿Entendemos bien el problema?
Aconsejamos su lectura detenida y pausada, haciéndonos preguntas como ¿qué conocemos?, ¿qué buscamos? Podemos hacer un esquema o dibujo del patio y anotar sus dimensiones, largo y ancho, conocidas también como base y altura. ¿Qué ocurre en un metro cuadrado? ¿Cuántas losas necesitamos? ¿Y para dos metros cuadrados?
2.- Llega el momento de trazar un plan
¿Lo tenemos? ¿Nos hemos enfrentado anteriormente a una situación similar? ¿Qué superficie o área total abarca el patio? Recordamos:
3.- Ponemos en marcha nuestro plan
Aconsejamos, en primer lugar, realizar algunas simulaciones previas con la unidad liberada de PISA que lleva el mismo título. Para ello, debemos pulsar el botón inicio hasta encontrar "El patio", realizamos los cálculos según el plan trazado y colocamos la solución en el campo superior derecho, sin olvidar redondear al valor entero más cercano. Finalmente, pulsamos el botón corregir. Podemos practicar las veces que necesitemos.
Volvemos a nuestro problema y ejecutamos el plan para encontrar la solución, comprobando cada paso con los miembros del equipo y anotando una pequeña explicación junto a cada operación matemática aclarando qué hacemos y qué conseguimos.
4.- Reflexionamos sobre el proceso y analizamos la solución obtenida
Leemos nuevamente el enunciado y nos aseguramos de que lo solicitado es lo que hemos averiguado. Nos preguntamos si la solución parece razonable y no olvidaremos indicar qué significa el valor obtenido como solución, en nuestro caso losas para el pavimento.
¿Creemos que en la vida real se compra la cantidad exacta de losas o debemos comprar algunas más para prevenir las que se romperán durante el enlosado?
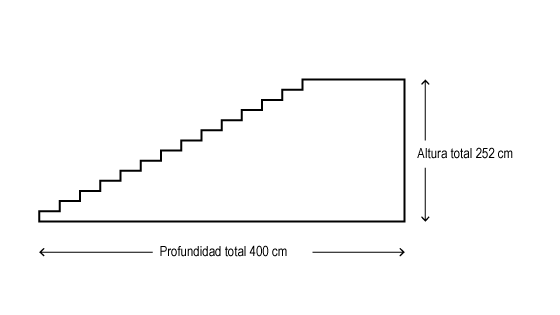
La escalera
1.- ¿Entendemos bien el problema?
Aconsejamos su lectura detenida y pausada, haciéndonos preguntas como ¿qué conocemos?, ¿qué buscamos? Podemos incluso imaginar que subimos por la escalera y apreciar las dos dimensiones que posee cada peldaño, es decir, una anchura, donde colocamos el pie, y la altura a la que debemos levantarlo. ¿Tenemos claro qué buscamos? ¿Son necesarios todos los datos que aporta esta situación para construir la escalera?
2.- Llega el momento de trazar un plan
¿Lo tenemos? ¿Nos hemos enfrentado anteriormente a una situación similar?
3.- Ponemos en marcha nuestro plan
Aconsejamos, en primer lugar, realizar algunas simulaciones previas con la unidad liberada de PISA que lleva el mismo título. Para ello, debemos pulsar el botón inicio y poner sumo cuidado en la lectura, ya que unas veces se pregunta por la altura del peldaño y otras por su anchura, realizamos los cálculos según el plan trazado y colocamos la solución en el campo superior derecho. Finalmente, pulsamos el botón corregir. Podemos practicar las veces que necesitemos.
Volvemos a nuestro problema y ejecutamos el plan para encontrar la solución, comprobando cada paso con los miembros del equipo y anotando una pequeña explicación junto a cada operación matemática aclarando qué hacemos y qué conseguimos.
4.- Reflexionamos sobre el proceso y analizamos la solución obtenida
Leemos nuevamente el enunciado y nos aseguramos de que lo solicitado es lo que hemos averiguado. Nos preguntamos si la solución parece razonable y no olvidaremos indicar la unidad de medida para la altura de cada peldaño. ¿Se puede comprobar la solución?
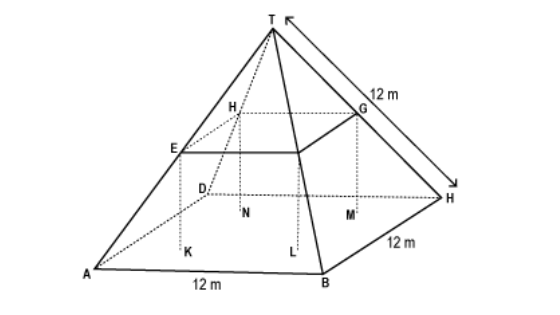
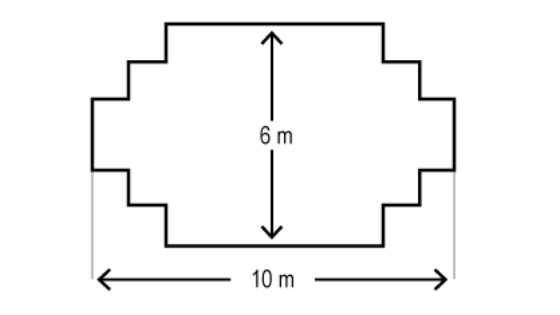
El ático y el desván
1.- ¿Entendemos bien el problema?
Aconsejamos su lectura detenida y pausada, haciéndonos preguntas como ¿qué conocemos?, ¿qué buscamos?
2.- Llega el momento de trazar un plan
¿Lo tenemos? ¿Nos hemos enfrentado anteriormente a una situación similar? ¿Hemos localizado el suelo del ático y el del desván? ¿Qué polígonos forman?
En caso de necesitar más ayuda, podemos realizar algunas simulaciones previas con la unidad liberada de PISA que lleva por título "Granjas".
3.- Ponemos en marcha nuestro plan
Ejecutamos el plan para encontrar la solución, comprobando cada paso con los miembros del equipo y anotando una pequeña explicación junto a cada operación matemática aclarando qué hacemos y qué conseguimos.
4.- Reflexionamos sobre el proceso y analizamos la solución obtenida
Leemos nuevamente el enunciado y nos aseguramos de que lo solicitado es lo que hemos averiguado. Nos preguntamos si la solución parece razonable y no olvidaremos indicar la unidad de medida, en este caso, compraremos el parqué por metros cuadrados.
¿Se puede comprobar la solución?
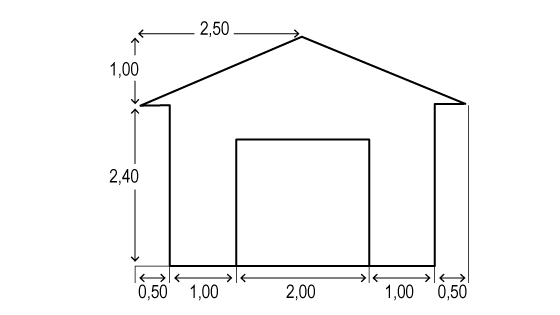
El garaje
1.- ¿Entendemos bien el problema?
Aconsejamos su lectura detenida y pausada, haciéndonos preguntas como ¿qué conocemos?, ¿qué buscamos?
2.- Llega el momento de trazar un plan
¿Lo tenemos? ¿Nos hemos enfrentado anteriormente a una situación similar? ¿Hemos localizado y calculado las dimensiones de cada ala del tejado? ¿Somos conscientes de que tendremos que aplicar el Teorema de Pitágoras?
En caso de necesitar más ayuda, podemos realizar algunas simulaciones previas con la unidad liberada de PISA que lleva el mismo título.
3.- Ponemos en marcha nuestro plan
Ejecutamos el plan para encontrar la solución, comprobando cada paso con los miembros del equipo y anotando una pequeña explicación junto a cada operación matemática aclarando qué hacemos y qué conseguimos.
4.- Reflexionamos sobre el proceso y analizamos la solución obtenida
Leemos nuevamente el enunciado y nos aseguramos de que lo solicitado es lo que hemos averiguado. Nos preguntamos si la solución parece razonable y no olvidaremos indicar la unidad de medida para la compra del material para el tejado, en este caso, metros cuadrados. ¿Se puede comprobar la solución?
El jardín
1.- ¿Entendemos bien el problema?
Aconsejamos su lectura detenida y pausada, haciéndonos preguntas como ¿qué conocemos?, ¿qué buscamos?
2.- Llega el momento de trazar un plan
¿Lo tenemos? ¿Nos hemos enfrentado anteriormente a una situación similar?
3.- Ponemos en marcha nuestro plan
Aconsejamos, en primer lugar, realizar algunas simulaciones previas con la unidad liberada de PISA que lleva por título "Carpintero". Para ello, debemos pulsar el botón inicio y elegir la opción "El carpintero", realizamos los cálculos según el plan trazado y respondemos afirmativa o negativamente desde los menús desplegables. Finalmente, pulsamos el botón corregir. Podemos practicar las veces que necesitemos.
Volvemos a nuestro problema y ejecutamos el plan para encontrar la solución, comprobando cada paso con los miembros del equipo y anotando una pequeña explicación junto a cada operación matemática aclarando qué hacemos y qué conseguimos.
4.- Reflexionamos sobre el proceso y analizamos la solución obtenida
Leemos nuevamente el enunciado y nos aseguramos de que lo solicitado es lo que hemos averiguado. Nos preguntamos si la solución parece razonable y no olvidaremos indicar la unidad de medida para la cantidad de valla.
¿Se puede comprobar la solución?
El pozo
1.- ¿Entendemos bien el problema?
Aconsejamos su lectura detenida y pausada, haciéndonos preguntas como ¿qué conocemos?, ¿qué buscamos? ¿Nos preguntan por la capacidad del pozo?
2.- Llega el momento de trazar un plan
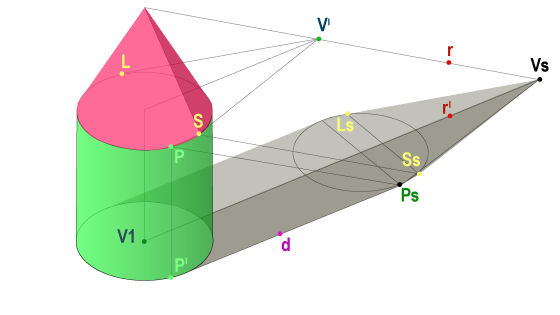
¿Lo tenemos? ¿Nos hemos enfrentado anteriormente a una situación similar? ¿Qué figura geométrica podemos usar que se ajuste a nuestra situación? ¿Un cono? ¿Un cilindro?
3.- Ponemos en marcha nuestro plan
Aconsejamos, en primer lugar, realizar algunas simulaciones previas con la unidad dedicada al "Área del cilindro", que posee una escena interactiva que nos permite conocer cómo se desarrolla el cilindro y nos explica la forma de obtener su área lateral. Incluso podemos obtener parte de la solución introduciendo las dimensiones de nuestro pozo. Ahora bien, el informe técnico debe recoger todos los cálculos y presupuestos detallados.
4.- Reflexionamos sobre el proceso y analizamos la solución obtenida
Leemos nuevamente el enunciado y nos aseguramos de que lo solicitado es lo que hemos averiguado. Nos preguntamos si la solución parece razonable y no olvidaremos indicar la unidad de moneda.
¿Se puede comprobar la solución?
El depósito de combustible
1.- ¿Entendemos bien el problema?
Aconsejamos su lectura detenida y pausada, haciéndonos preguntas como ¿qué conocemos?, ¿qué buscamos? En esta ocasión, buscamos la capacidad del depósito, es decir, su volumen.
2.- Llega el momento de trazar un plan
¿Lo tenemos? ¿Nos hemos enfrentado anteriormente a una situación similar? ¿Qué figura geométrica podemos usar que se ajuste a nuestra situación? ¿Un cono? ¿Un cilindro? ¿Ambos?
3.- Ponemos en marcha nuestro plan
Aconsejamos, en primer lugar, realizar algunas simulaciones previas con la unidad dedicada al "Volumen del cilindro" y al "Volumen del cono", que posee escenas interactivas que nos permiten conocer cómo se desarrolla estos cuerpos de revolución y nos explica la forma de obtener sus volúmenes.
Por si fuera necesario, proporcionamos un enlace al recurso "Capacidad y volumen", que nos recuerda la relación entre litros y m³.
4.- Reflexionamos sobre el proceso y analizamos la solución obtenida
Leemos nuevamente el enunciado y nos aseguramos de que lo solicitado es lo que hemos averiguado. Nos preguntamos si la solución parece razonable y no olvidaremos indicar la unidad de medida.
¿Se puede comprobar la solución?
La piscina
1.- ¿Entendemos bien el problema?
Aconsejamos su lectura detenida y pausada, haciéndonos preguntas como ¿qué conocemos?, ¿qué buscamos? En esta ocasión, buscamos la capacidad de la piscina, es decir, su volumen.
2.- Llega el momento de trazar un plan
¿Lo tenemos? ¿Nos hemos enfrentado anteriormente a una situación similar? ¿Conocemos alguna piscina de similares dimensiones y su capacidad para hacer una estimación previa? ¿Qué forma poliédrica tiene la piscina? ¿Un prisma?
3.- Ponemos en marcha nuestro plan
Aconsejamos, en primer lugar, realizar algunas simulaciones previas con la unidad dedicada al "Volumen de un prisma recto", que nos recuerda cómo hallar su volumen.
Por si fuera necesario, proporcionamos un enlace al recurso "Capacidad y volumen", que nos recuerda la relación entre litros y m³, así como "Unidades de volumen".
También podemos usar el "Conversor para calcular los litros de una piscina rectangular", y así sabremos la solución automáticamente. Ahora, bien tenemos que justificar los cálculos en nuestro informe técnico.
4.- Reflexionamos sobre el proceso y analizamos la solución obtenida
Leemos nuevamente el enunciado y nos aseguramos de que lo solicitado es lo que hemos averiguado. Nos preguntamos si la solución parece razonable y no olvidaremos indicar la unidad de medida.
¿Se corresponde la solución con la estimación previa?