1.1. Líneas en la esfera
|
|
|
Transportador de Ángulos. Animación de Juan García Moreno en el banco de imágenes del ITE
Licencia Creative Commons by-nc-sa |
¿Recuerdas cómo se medían los ángulos? Puedes practicar en la ventana interactiva de arriba utilizando el transportador.
¿Conoces algunas de las propiedades de los ángulos? Como yo no recuerdo muchas cosas sobre la medición de ángulos, en este caso te voy a pedir que realices primero una investigación y después me expongas tus resultados. Más concretamente necesito que me pases por correo electrónico un documento en pdf que hayas elaborado y en el que me expliques cómo se mide un ángulo, las unidades de medida que se utilizan, cómo pasar de una a otra y qué significan estas medidas cuando aparecen decimales.
Creo recordar que algo raro pasaba en estos casos.
Tu documento deberá contener imágenes explicativas que ilustren aquello que me estés indicando. Explícame también el ángulo de una circunferencia, el de media y el de un cuarto de circunferencia.
a) 37,14º son º ' y ''.
b) -23,12º son º ' y ''.
c) 45,56º son º ' y ''.
d) Si sumamos los ángulos 32º 24' 48" y 43º 49' 25" nos resulta el ángulo º ' y " .
e) Si al ángulo 52º 23' 18" le restamos el ángulo 43º 49' y 25" nos resulta el ángulo º ' y "
f) 180.500" son º ' y "
g) 23º 30' y 12" son º
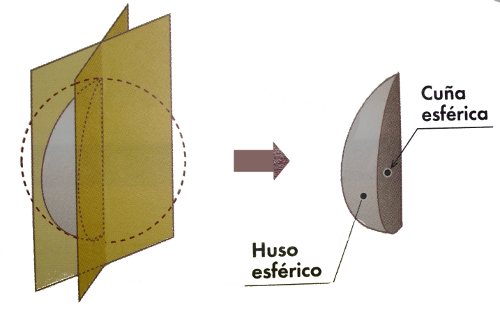 |
| Huso esférico. Imagen de Mariano Real Pérez en Flickr.Licencia Creative Commons by-nc-sa |
 |
|
Corte por planos paralelos. Imagen de Mariano Real Pérez en Flickr.
Licencia Creative Commons by-nc-sa
|
Ahora vamos a ver diferentes formas de hacer cortes en una esfera:
Si en una esfera realizamos dos cortes con planos que tengan en común un mismo eje de la esfera, obtenemos una figura en forma de gajo de naranja (como la que observamos en la imagen de la derecha). La parte externa de ese gajo recibe el nombre de huso esférico y el gajo propiamente dicho recibe el nombre de cuña esférica. En la imagen podemos observa cada una de ellas.
Otro posible corte que podríamos efectuar en la esfera sería por planos paralelos. En la segunda imagen de la derecha podemos observar cómo sería ese corte y las zonas en las que quedaría dividida la esfera. Por un lado nos quedaría la parte superior que se denomina casquete esférico y por otro lado nos quedaría el trozo de la esfera entre plano y plano que se denomina zona esférica.
Estos son los dos cortes más importantes y que nos van a interesar en nuestro desarrollo.
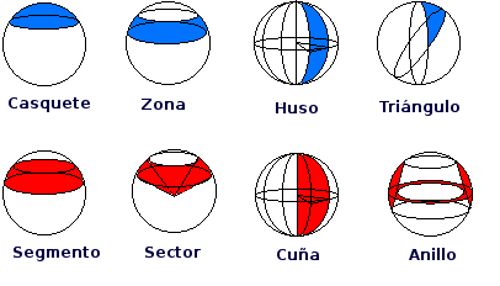
Existen otros que podemos observar en la siguiente imagen y cuyo nombre también se indica:
 |
|
Cortes en la esfera. Imagen de Mariano Real Pérez en Flickr.
Licencia Creative Commons by-nc-sa
|
En la siguiente ventana interactiva podemos observar las divisiones que nos resultan en una esfera a partir de 24 husos y 24 planos paralelos. Mueve la esfera arrastrando el ratón.
| Esfera interactiva. Imagen interactiva de Marta Oliveró y José Luis Abreu en la aplicación Superficies en 3D que encuentra en la web del ITE.
Licencia Creative Commons by-nc-sa |
Has visto dos formas de realizar cortes en una esfera. Pero ¿hasta dónde podemos llegar?
De las siguientes afirmaciones que aparecen, selecciona las que consideres correctas. Coméntalas posteriormente con tus compañeros aportando las razones de tu elección.
 |
|
Zumo de naranja. Imagen del ITE en el banco de imágenes del ITE
Licencia Creative Commons by-nc-sa |
¿Cuándo utilizamos esferas?
Si observas a tu alrededor seguramente puedas apreciar gran cantidad de situaciones en las que utilizamos el huso esférico, la cuña esférica, el casquete esférico o la zona esférica.
Fotografía al menos 6 ejemplos de esta utilización.
Realiza una exposición oral a tus compañeros en la que expliques el tipo de corte en la esfera de que se trata.
Curiosidad
|
|
|
Divisiones reales sobre una esfera. Video de Mariano Real en Youtube.
Licencia Creative Commons by |
Por otra parte, el logotipo utilizado en la exposición universal de Sevilla en 1992 y que puedes observar más abajo también nos muestra la división de una esfera, utilizando las dos divisiones tratadas más arriba.
Investiga cuántos planos paralelos y cuántos planos que utilizan el mismo eje de la esfera se han utilizado para hacer las divisiones que aparecen.
 |
|
Divisiones del logo de la Expo'92. Imagen de Mariano Real Pérez en Flickr.
Licencia Creative Commons by-nc-sa |