1.2. Divisiones verticales y horizontales
Sobre la Tierra vamos a construir una malla que nos sirva de sistema de referencia. Para ello vamos a utilizar las dos formas que tenemos de cortar una esfera, vistas en el apartado anterior. En este caso concreto, sobre la esfera terráquea, disponemos de un eje que nos va a servir para realizar las divisiones. Este eje es el de rotación de la Tierra.
Observa el siguiente vídeo.
|
|
|
Líneas de división sobre la Tierra. Video de mariano31415 en Youtube.
Licencia Creative Commons by-nc-sa. |
A partir de ese eje de rotación, vamos a denominar meridiano a la circunferencia imaginaria que aparece al cortar la Tierra con un plano que contenga al eje de rotación de la Tierra. Todas estas circunferencias son iguales en longitud. Todas ellas pasa por los polos.
 |
| Paralelos y meridianos. Imagen de José Alberto Bermúdez en el banco de imágenes del ITELicencia Creative Commons by-nc-sa |
Por otra parte, vamos a denominar paralelo a la circunferencia imaginaria que aparece al cortar la esfera terráquea con un plano perpendicular al eje de rotación. En este caso, no todas las circunferencias que aparecen tienen la misma longitud. Una de ellas tiene mayor longitud, se denomina ecuador. Esta línea divide a la Tierra en dos partes iguales: norte y sur.
Tarea
 |
Investiga sobre la etimología de las palabras meridiano y ecuador. Indica, según los contenidos que estás viendo, qué definición es la más apropiada para cada una de estas palabras.
Responde a cada una de las siguientes preguntas, anotando la respuesta en tu cuaderno.
- ¿Crees que cada una de estas líneas tiene la misma longitud?
- ¿Qué longitud tiene la línea del ecuador?
- ¿A qué distancia te encuentras del centro de la Tierra?
Julio Verne, fue un escritor francés de novelas de aventuras. Es considerado uno de los padres de la ciencia ficción. Es el segundo autor más traducido de todos los tiempos con 4185 traducciones. Algunas de sus obras han sido adaptadas al cine. Predijo con gran exactitud en sus relatos fantásticos la aparición de algunos de los productos generados por el avance tecnológico del siglo XX, como la televisión, los helicópteros, los submarinos o las naves espaciales. Uno de sus libros lleva por título "viaje al centro de la Tierra".
Intenta investigar sobre el contenido de esta novela. ¿Crees que algún día se llegará al centro de la Tierra como ha sucedido con alguna otra hazaña sobre las que escribió sin que fueran realidad? Argumenta tu respuesta.
Anota en tu cuaderno los datos, cálculos y conclusiones a las que hayas llegado con las preguntas anteriores y debate con tus compañeros sobre las mismas. Recuerda argumentar debidamente los aspectos científicos de cada una de ellas.
En esta actividad vamos a utilizar la ventana interactiva que aparece más abajo. Aquí podrás profundizar en el significado de meridianos y paralelos. En todo momento supondremos, para simplificar, que la Tierra es una esfera perfecta.
|
|
| Meridianos y parelelos.Construcción de Rafael Losada Liste y José Luis Álvarez García en el proyecto Gauss Licencia Creative Commons by-nc-sa |
1.- Pulsa el botón de Reproducir-Parar cada vez que quieras girar la Tierra. Observando las marcas de cada octante, en el ecuador, ¿cuántos grados separa un meridiano del siguiente?
Activa la casilla Punto y compruébalo moviendo el punto de uno a otro (usa las teclas + y - para aumentar la precisión).
2.- Por tanto, ¿cuántos meridianos (semicircunferencias de polo a polo) aparecen representados en total en toda la Tierra?
3.- ¿Tienen todos los meridianos la misma longitud? ¿Por qué? ¿Dónde se encuentra el centro de todos ellos?
4.- Los meridianos se denominan por su ángulo: meridiano 0 (o meridiano de Greenwich), meridiano 15, meridiano -15, etc. Localiza un país por donde pase el meridiano 150.
6.- Por tanto, ¿cuántos paralelos (excluyendo al ecuador, que sería el "paralelo 0") aparecen representados en total en toda la Tierra (incluidos los más cercanos al Polo Sur, aunque no sean visibles)?
Anota en tu cuaderno la respuesta a cada una de estas preguntas. Seguidamente, debate con tus compañeros sobre la respuesta que has dado a cada una.
Anota la respuesta a todas estas preguntas en tu cuaderno y cuando hallas terminado comparte la solución con el resto de compañeros exponiendo tus conclusiones.
Tarea
 |
|
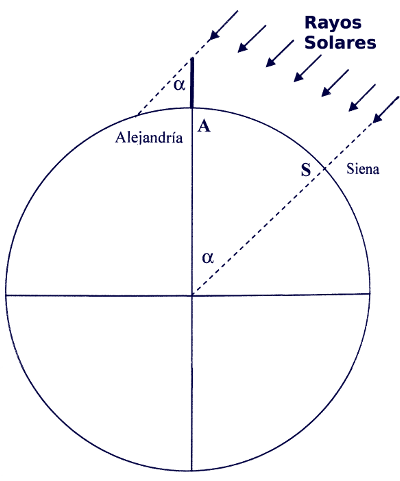
Imagen de la hipótesis de Eratóstenes. Imagen de Mariano Real Pérez en Flickr.
Licencia Creative Commons by-nc-sa. |
Eratóstenes, matemático griego del siglo III antes de Cristo, diseñó un sencillo método geométrico con el que pudo determinar la longitud de la circunferencia de la Tierra.
Para hacerlo se basó en cuatro hipótesis:
a) Las ciudades de Siena y Alejandría están situadas sobre un mismo meridiano.
b) El día 21 de junio, cuando se produce el solsticio de verano, al mediodía, los rayos del Sol se reflejan en el fondo de un profundo pozo de Siena. por tanto, en Siena ese día y a esa hora los objetos no dan sombra.
c) La distancia entre Siena y Alejandría es de 5.000 estadios.
d) Los rayos solares son paralelos.
Con estos supuestos, Eratóstenes pudo deducir que el ángulo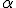 
que forman los rayos de Sol con la vertical en Alejandría era de 7º y 12', es decir 
. De esto resulta que, si dividimos la longitud del arco que separa Alejandría de Siena 
entre la longitud total de la circunferencia de la Tierra, 
, el resultado debe ser que:
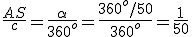
Por tanto tenemos que la circunferencia de la Tierra es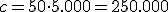 
estadios.
Eratóstenes se basó en las hipótesis que te hemos plateado anteriormente, pero no todas son ciertas. Localiza aquella o aquellas que sean erróneas y anótalas en tu cuaderno.
Calcula en unidades conocidas la distancia entre Siena y Alejandría en la que se basó Eratóstenes. Calcula también la longitud de la circunferencia de la Tierra que estableció.
Con esta medida dada por Eratóstenes se estableció una medida internacional que se denominó metro. Investiga a qué equivalía un metro a partir de este estudio.
Crea una presentación con la respuesta a las anteriores preguntas, ilustrándola con imágenes aclaratorias y súbela a Internet.
Crea una entrada en el blog de aula en la que aparezca incrustada la presentación que has realizado. Colócale a esta entrada dos etiquetas. La primera formada a partir de la primera letra de tu nombre y el primer apellido (por ejemplo, de Mariano Real sería mreal). Como segunda etiqueta el nombre del matemático que estás estudiando.
