Cuando dos rectas se encuentran o no
En la siguiente escena, tienes representadas dos rectas que pueden corresponder a dos funciones lineales o afines.
Manipula los deslizadores y podrás representar las gráficas de distintas funciones. En concreto, construye los siguientes pares de funciones y anota en tu cuaderno qué efecto tienen sobre las gráficas.
a) 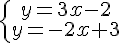 b)
b) 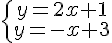 c)
c) 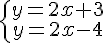 d)
d) 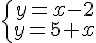 e)
e) 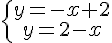
Importante
 |
- Las dos líneas se cortan en un punto, esto ocurre cuando las dos rectas tienen distinta pendiente.
- Las dos líneas son paralelas. En este caso, las funciones tienen la misma pendiente pero distinta ordenada en el origen.
- Las dos rectas coinciden, en cuyo caso las funciones tienen los mismos coeficientes, tanto para la pendiente como para la ordenada en el origen.
Hay veces en que el punto de corte de las dos funciones es fácil de observar al representar las dos gráficas. Así pasa en el apartado a) que has aplicado antes en el applet de Geogebra. Pero, otras veces, no es tan evidente; sobre todo cuando el punto de corte no tiene coordenadas enteras, como ocurre en el apartado b).
En estos casos, lo que debemos hacer es hallar el punto de corte por métodos algebraicos. La ventaja para ti es que es algo que ya has aprendido hace meses. Para saber cuál es el punto de corte, basta con que resuelvas el sistema formado por las dos ecuaciones que representan a cada función; algo que aprendiste en la Unidad 4 (cuando trabajaste los sistemas de ecuaciones).
Según la expresión que tengamos en las funciones, se puede utilizar uno u otro método de resolución. Si las funciones están en forma explícita, lo mejor es utilizar el método de igualación. Si están en forma implícita, el método más adecuado es el de reducción.
Ten presente siempre que la solución del sistema es un par de valores que verifican las dos ecuaciones a la vez.
Comprueba lo aprendido
Tarea

En el mundo de la ciencia es muy corriente encontrar expresiones funcionales en casi cualquier situación. No sabemos si habrás visitado alguna vez un laboratorio de física o química y habrás hecho algún experimento, pero es corriente que la relación entre los productos que se manipulan y la energía que necesitamos para modificar esos elementos sean relaciones lineales. Vamos a trabajar con una de ellas en esta ocasión.
La energía térmica, o calorífica, de cada cuerpo depende del movimiento de sus partículas y podemos medirla a través de su temperatura. Si queremos modificar, aumentando, por ejemplo, esa energía térmica, necesitamos aplicar una cierta energía que depende de la cantidad de masa que estemos utilizando y de una constante llamada calor específico que depende del material con que esté hecho el cuerpo al que le queremos modificar su temperatura.
Supongamos que vamos a realizar un experimento. Tenemos dos varillas de 100 g cada una. La primera es de plomo y la segunda es de hierro. La varilla de plomo la tenemos a 20ºC y la de hierro a 50ºC y comenzamos a calentar ambas varillas. Queremos que ambas alcancen la misma temperatura.
Investiga cuál es el momento en que tienen la misma temperatura y cuánta energía hemos necesitado para llevar ambos materiales a la misma temperatura final.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0