Seguimos recto
Si te paras a pensar, encontrarás multitud de situaciones en las que hay funciones lineales en tu entorno diario. Sin embargo, no siempre podemos encontrar este tipo de relación aunque se represente también mediante una línea recta. Por ejemplo, si en casa tienes contador de agua, al mirar la factura podrás encontrar que, aparte de la cantidad de agua que se ha gastado ese mes nos aparece una cantidad fija correspondiente al alquiler de los contadores y el servicio que se nos suministra. Por lo tanto, lo que hay que pagar ya no es directamente proporcional al gasto de agua. Esta misma situación se repite en muchos otros servicios del hogar, como en la luz o en el teléfono fijo.
Recuerda el ejemplo que pusimos en el apartado 1 de la compra del pan. Ya comentamos que cada pieza de pan valía 0,35 euros, por ello la función que relacionaba el número de piezas compradas con el gasto de la compra era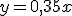 
. Pero imagínate que tienes que comprar muchas piezas, como para llevarlas en la mano, y se te ha olvidado llevar una bolsa de casa. Por tanto, tienes que comprar allí una bolsa, pues ya sabrás que desde hace tiempo ya no regalan las bolsas si no, que hay que comprarlas. Por la bolsa te piden 0.05 euros. En ese caso la función cambia y lo que debes pagar se convierte en 
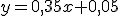, que está claro que ya no es una función de proporcionalidad directa.
La forma más fácil de verlo es tener en cuenta que; en este tipo de funciones, si hacemos 0 la variable independiente x, la variable dependiente ya no vale cero. En este caso, desde el momento en que pedimos la bolsa, ya le debemos a la panadera 5 céntimos, independientemente del número de piezas de pan que compremos.
Importante
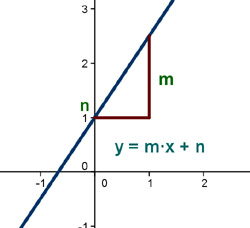
Una función lineal a la que se le suma o resta una constante, que no depende de la variable, se convierte en una función afín; cuya expresión general es de la forma:
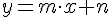
Toda función afín lleva asociada una gráfica que es una línea recta, pero que no pasa ya por el origen de coordenadas.
El coeficiente de la x (m) sigue siendo la pendiente de la recta.
Si en esa función hacemos x cero, el valor que le corresponde será n y, por tanto, la gráfica de la función pasará por el punto (0,n). Este punto es donde la gráfica de la función corta al eje vertical, por eso n recibe el nombre de ordenada en el origen.
En la siguiente escena puedes ver una función afín.
Si mueves los deslizadores m y n representarás otra función afín. Puedes observar que el término independiente de la expresión de la función siempre coincide con el valor del punto de corte con el eje vertical.
Si mueves los puntos P y Q por la recta observarás que se verifica que el cociente entre la diferencia entre las ordenadas del punto P y Q y la diferencia de las abscisas correspondientes es siempre el valor de la pendiente de la función lineal.
En particular, puedes observar que la pendiente es el valor que aumenta la y cuando la x aumenta una unidad.
Para saber más
 |
Para practicar como hallar la expresión de la función afín a partir de su gráfica puedes trabajar con los ejemplos a los que accedes desde el siguiente enlace. Observa algunos ejemplos y copia en tu cuaderno el desarrollo de dos ejemplos de función afín crecientes y otras dos decrecientes. |
Comprueba lo aprendido
Las gráficas que aparecen se corresponden con cuatro funciones afines. Cada una de ellas corresponde a una de las siguientes expresiones algebraicas.
a)  |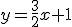
b)  |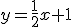
c)  |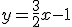
d)  |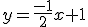
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0