Distintas expresiones para la ecuación de una recta
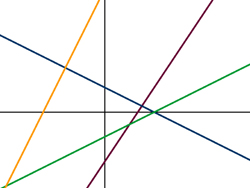 |
Ya hemos visto que la expresión 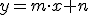 representa una función cuya gráfica es una línea recta. Esa ecuación, por lo tanto, representa la ecuación de una recta. Como veremos en este apartado, existen otras expresiones equivalentes. La expresión anterior recibe el nombre de forma explicita de la ecuación de la recta.
representa una función cuya gráfica es una línea recta. Esa ecuación, por lo tanto, representa la ecuación de una recta. Como veremos en este apartado, existen otras expresiones equivalentes. La expresión anterior recibe el nombre de forma explicita de la ecuación de la recta.
Conocemos ya varias formas de hallar esa ecuación. En particular, hemos visto que el método más simple puede aplicarse cuando conocemos la pendiente y la ordenada en el origen. En el caso de que conociéramos dos puntos por donde pasa, también hemos estudiado cómo hallar su pendiente. En concreto, si la recta pasa por los puntos 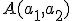 y
y 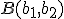 , la forma de hallar la pendiente es muy fácil; ya que basta dividir la variación que hay en la ordenada, al pasar de un punto a otro, entre la variación de la abscisa. Es decir, la pendiente sería:
, la forma de hallar la pendiente es muy fácil; ya que basta dividir la variación que hay en la ordenada, al pasar de un punto a otro, entre la variación de la abscisa. Es decir, la pendiente sería:
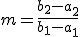
Da lo mismo el orden en que se elijan los puntos, pero debe ser el mismo en los dos miembros de la fracción. En el siguiente ejercicio resuelto puedes ver cómo calcular la ecuación de la recta que pasa por dos puntos de diversas maneras.
Aprende a hacerlo
a) (2,5), (0,1)
b) (-1,5), (3,1)
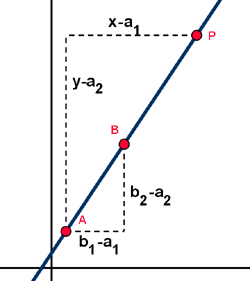 |
Sin embargo, si conocemos dos puntos de la recta podemos hallar la ecuación de una forma directa. Para ello vamos a utilizar la semejanza de triángulos.
Vamos a suponer que tenemos dos puntos de la recta que son conocidos, 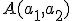 y
y 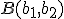 . Además vamos a considerar un punto genérico
. Además vamos a considerar un punto genérico 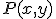 que representará a todos los puntos de la recta.
que representará a todos los puntos de la recta.
Si te fijas en la imagen, verás que hay una razón de semejanza entre los cambios para pasar del punto A al B y los cambios para pasar del punto A al P. Imponiendo que existe una proporción entre esas cantidades, llegamos a la expresión siguiente:
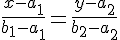
Esta expresión de la ecuación de la recta que pasa por dos puntos suele recibir el nombre de forma continua de la ecuación de la recta. Si operamos en esa expresión y despejamos la incógnita, llegamos a la forma explícita que hemos visto hasta el momento.
Aprende a hacerlo
En la red
|
En el siguiente enlace puedes encontrar más ejemplos de cálculo de la expresión continua de una recta (para pasar a continuación a su forma explícita y hallar su pendiente y su ordenada en el origen). Copia en tu cuaderno un ejemplo resuelto de función con pendiente positiva, otra negativa y uno de ecuación de una recta que no representa a una función. |
 |
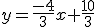 . Si multiplicamos por 3 estábamos en la expresión
. Si multiplicamos por 3 estábamos en la expresión 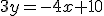 .
.
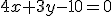 . Como podemos ver es una expresión en la que todos los términos están mezclados en el primer miembro, es decir, no hay ninguna variable despejada como ocurría en la forma explícita.
. Como podemos ver es una expresión en la que todos los términos están mezclados en el primer miembro, es decir, no hay ninguna variable despejada como ocurría en la forma explícita.
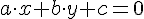 .
.
En la red
 |
Para practicar todas estas expresiones distintas de la ecuación de una recta, puedes ir al siguiente enlace. En él encontrarás ejercicios resueltos de tres tipos distintos:
|
Copia en tu cuaderno al menos uno de cada tipo.
Tarea
¿Relacionamos?
Ahora vas a hacer matemáticas como si tu fueses el profesor. Vas a aplicar todo lo que aprendiste en la parte de álgebra para deducir lo siguiente: que relación existe entre la pendiente y la ordenada en el origen de la ecuación de una recta y las constantes a, b y c de su expresión general.
Es decir, debes partir de la expresión 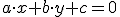 y, tras despejar el valor de y, escribir m y n en función de a, b y c.
y, tras despejar el valor de y, escribir m y n en función de a, b y c.
En el ejercicio resuelto que has trabajado antes, has visto cómo era posible encontrar la ecuación de una recta a partir de dos puntos: hallando primero la pendiente y después, con uno cualquiera de los puntos, encontrando el valor de la ordenada en el origen.
Pero en el caso de que tengamos un punto por donde pasa la gráfica de la función y la pendiente, hay una forma más rápida de encontrar otra expresión de la ecuación.
El razonamiento es muy parecido a lo que hemos visto anteriormente. Supongamos que tenemos un punto Q(a,b) y un punto genérico de la recta P(x,y) y además sabemos que la pendiente es m. Como ya has aprendido antes, teniendo dos puntos podemos sacar fácilmente la pendiente, luego con P y Q podemos hallar la pendiente que será:
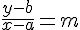
Si en la expresión anterior despejamos, obtenemos dos expresiones equivalentes que se conocen como la forma punto-pendiente de la ecuación de la recta.
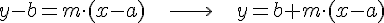
Comprueba lo aprendido
Solución
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0