Sin variación

José Muñoz. Carrusel.

Hay situaciones cotidianas en las que también nos encontramos con funciones cuya representación es una línea recta, pero que son un caso particular de las funciones lineales o afines que hemos visto en los apartados anteriores. Te ponemos un ejemplo. Si eres aficionado a asistir a las fiestas y ferias tradicionales de tu población, seguramente te gustará montarte en las atracciones de feria que hayan traído para esa celebración. Si suponemos que todas las atracciones tienen el mismo coste, la función que te da lo que te gastas en función del número de atracciones que visitas es una función lineal. Sin embargo, si asistes a un parque temático, la entrada tiene precio único y con ella puedes montarte en todas las atracciones que quieras, por lo que la función que te da la relación anterior es una constante.

Algo parecido pasa con las líneas de teléfono. No es lo mismo tener un contrato en el que pagas por minutos hablado que una tarifa plana que pagas lo mismo al mes hayas hablado la cantidad de minutos que sea.

Sobre esos valores constantes vamos a tratar en este apartado. Antes de seguir es conveniente que vuelves al apartado anterior y manipules la ventana de Geogebra que tenías. ¿Qué ocurre con la gráfica de la función si la pendiente se hace cero?

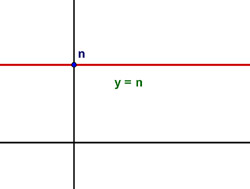Si tenemos una función afín en la que la pendiente se anula, habrás observado que la gráfica de la función se convierte en una línea horizontal, es decir, paralela al eje de abscisas. Cuando ocurre esto decimos que la función es constante ya que para todo valor que se le dé a la variable independiente x se obtiene siempre el mismo valor.

La función constante tiene la expresión:

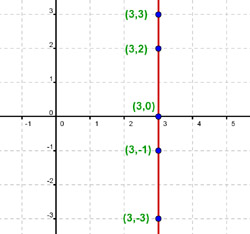Dentro de las líneas rectas hay una en particular que guarda cierto parecido con la función constante. Nos referimos a una línea recta que sea vertical, es decir, paralela al eje de ordenadas. Este tipo de líneas será bastante habitual en los próximos cursos que tengas de matemáticas.

Si te fijas en la figura, la recta que aparece representada tiene la característica de que todos sus puntos tienen como primera componente el valor x = 3, por ello se indica que su ecuación es precisamente x=3.

Sí debes tener siempre presente que esa línea no representa a una función, ya que en una función no puede haber más de un valor distinto para el mismo valor de la variable independiente.

Para ver si tienes clara la diferencia entre los cuatro tipos de gráficas representadas por líneas rectas, realiza la siguiente actividad.