4.1. Potencias de exponente natural
Comprueba lo aprendido
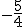deberás escribir -5/4 en el hueco en blanco.
|
|
| Fracciones de la unidad. Animación de Juan García Moreno en Banco de imágenes del ITE Licencia Creatibe Commons by-nc-sa |
Antes de comenzar con las operaciones, si quieres puedes observar en la imagen interactiva la representación gráfica de un número fraccionario.
Ahora te pedimos que completes los siguientes huecos en blanco indicando el resultado de cada una de las operaciones que te proponemos:
 =
|
|
|
 =
|
|
|
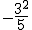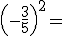
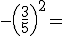
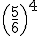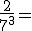
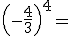
Ahora que has osado aventurarte en el mundo de las potencias de números fraccionarios, nos gustaría aclararte un poco las dificultades con las que te puedes encontrar. Por este motivo te hemos preparado el siguiente vídeo que te aconsejamos que observes.
|
|
|
Potencia de números racionales. Vídeo de juanmemol en Youtube.
Licencia Creative Commons by-nc-nd. |
Recuerda que todas las propiedades de las potencias que aparecían en el vídeo de Troncho y Poncho se siguen cumpliendo para las potencias de fracciones.
Una vez visionado, reflexiona sobre el mismo planteándote operaciones como las que has contemplado e intentando resolverlas. Como has practicado en puntos anteriores la forma de obtener la fracción generatriz de un número fraccionario, te pedimos también que calcules la fracción resultante de cada una de las siguientes operaciones:
;
;
;
|
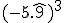
¿Es cierto que un número siempre es más grande que su cuadrado? Realiza una pequeña investigación, argumenta la respuesta en tu libreta y debate sobre el tema con tus compañeros y compañeras de clase |
Aprende a hacerlo
|
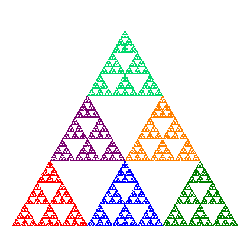
| Triángulo de Sierpinski. Imagen de Mariano Real. Licencia Creative Commons by-sa. |
Ahora vamos a estudiar una construcción muy curiosa que se llama el triángulo de Sierpinski. En el siguiente enlace puedes encontrar más información sobre este tipo de triángulo.
Vamos a partir de un triángulo equilátero de lado 12. Dibújalo en una hoja y construye el primer paso del triángulo de Sierpinski. Construye ahora el segundo. Y el tercero y el cuarto.
Investiga sobre la longitud del lado de los triángulos que aparecen en el primer paso, en el segundo y en el tercero. ¿Sabrías calcular la longitud de los lados de los triángulos que aparecen en el paso 10 y en el 12?
Centra tu estudio ahora en el área del triángulo (acuérdate de nuestro amigo Pitágoras). ¿Sabrías calcular el área del primer triángulo equilátero? ¿Cuántos triángulos equiláteros aparecen en el primer paso? ¿Sabrías calcular el área de cada uno de ellos? ¿Sabrías calcular el área de cada uno de los triángulos equiláteros que aparecen en el paso 5?
TRIÁNGULO DE SIERPINSKY
Para dibujar el triángulo de Sierpinsky, se parte de un triángulo. Se marcan los puntos medios de los lados que son los vértices de un triángulo invertido respecto al inicial. Nos resultan así tres nuevos triángulos en la misma posición que el inicial con los que volvemos a reiterar el proceso. Al repetir iterativamente este proceso, obtenemos el triángulo de Sierpinsky.
En el siguiente cuadro, se dibuja el triángulo de Sierpinsky por el método del caos: Se toman tres puntos en el plano que van a ser los vértices del triángulo de Sierpinsky. Se toma un punto aleatorio del plano, se selecciona aleatoriamente uno de los vértices, y se pinta el punto medio, que ahora tomará el papel del punto aleatorio inicial. Si los 1000 primeros puntos no se dibujan, pero los restantes siguiente sí, obtenemos el triángulo de Sierpinsky. En el cuadro hay que indicar el número de puntos que se desean dibujar, y una vez indicado basta con pulsar la tecla Aceptar para que se dibujen.
