1.1 Población y muestra
Importante
Veamos ahora los conceptos básicos de estadística que debes saber manejar:
- Población: es el conjunto de elementos que son objeto de estudio estadístico.
- Individuo: cada uno de los elementos de la población. El número total de individuos de la población se suele representar por la letra N.
Aunque tengan estos nombres, esos elementos pueden referirse a cualquier cosa y no solo a personas. Por ejemplo, podemos estudiar los televisores que se montan en una determinada fábrica, la cantidad de vehículos que se desplazan por carretera un fin de semana de agosto, o los programas de televisión más vistos en una determinada franja horaria. Cada televisor, vehículo o programa televisivo sería un individuo de ese estudio.
|
|
|
Pinchitos. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa |
A veces, es necesario estudiar a todos los individuos de la población. En este caso se trata de un estudio exhaustivo. Por ejemplo, cuando se realiza el censo de población de una determinada ciudad. En general, es muy costoso, en tiempo y dinero; entrevistar a todos los elementos objeto del estudio. Por ello, se selecciona solo una parte y en este caso se dice que se trata de un estudio muestral.
- Muestra: es una parte de la población con la que realmente se realiza el estudio.
- Tamaño: es el número de elementos del que se compone la muestra y se suele representar por la letra n.
La elección de la muestra es muy importante para que los resultados que se extraigan de ella se puedan generalizar a toda la población. Debe haber pocos individuos, para que no sea muy costosa su realización, pero elegidos de forma que aparezcan todos los estratos diferentes que forman la población. Por ejemplo, si quisiéramos saber los gustos culinarios de la juventud actual; no bastaría preguntar a las puertas de una pizzería, pues hay una parte de jóvenes que prefieren otro tipo de comidas y no visitan este tipo de establecimientos. Si lo hiciéramos, la muestra seleccionada no sería representativa de toda la población a estudiar.
En la red
|
Visita el siguiente enlace y comprueba si has asimilado los conceptos anteriores, para lo cual debes resolver el pasatiempo de palabras cruzadas. Si tienes problemas con alguno de los conceptos, vuelve a revisar las definiciones. |
Importante

|
|
Bolas numeradas para jugar al bingo de la sala Canoe, Madrid.
Imagen de Luana Fischer Ferreira en el banco de imágenes del ITE. Licencia Creative Commons by-nc-sa |
Para seleccionar la muestra, se suele utilizar el método aleatorio; consistente en elegir al azar a los individuos de un listado en el que se encuentran numerados todos los integrantes de la población que queremos estudiar.
La selección aleatoria se puede hacer de diversas formas: con bolas o papeletas numeradas introducidas en una una bolsa o caja (cuando el tamaño de la muestra es pequeño) o mediante una calculadora científica o programas informáticos, que utilizan funciones matemáticas que nos devuelven números al azar.
Generación aleatoria con calculadora: La generación aleatoria de un número entre 0 y 1 mediante una calculadora científica se realiza mediante la tecla RAN# (en ciertas calculadoras hay que pulsar previamente la tecla de segunda función SHIFT o INV). El número que nos devuelve es un número de tres cifras decimales. Si queremos obtener un número entero aleatorio entre 1 y n bastará con multiplicar el número obtenido por el número n, sumarle 1 y tomar la parte entera.
Si, por ejemplo, queremos obtener un número entero aleatorio entre 1 y 200 realizaríamos los siguientes pasos:
1) Pulsamos las teclas SHIFT RAN # y por ejemplo nos devuelve 0,644
2) Multiplicamos 0,644 por 200 y obtenemos 128,8
3) Sumamos 1 a 128,8 y obtenemos 129,8
4) Tomamos la parte entera 129. Por tanto 129 es el número obtenido aleatoriamente.
Como tarea; obtén, mediante el procedimiento anterior, cinco números enteros aleatorios entre 1 y 500. Anota en tu cuaderno los cálculos realizados y los números generados.
Generación aleatoria mediante la hoja de cálculo del paquete ofimático OpenOffice
En OpenOffice disponemos de dos funciones que nos permiten obtener números aleatorios.
- ALEATORIO(): devuelve un número aleatorio entre 0 y 1.
- ALEATORIO.ENTRE(n1;n2): devuelve un número entero entre n1 y n2 incluidos ambos números. Por ejemplo, si queremos obtener un número entero aleatorio entre 1 y 100, escribiríamos en la celda en la que queremos obtener dicho número =ALEATORIO.ENTRE(1;100)
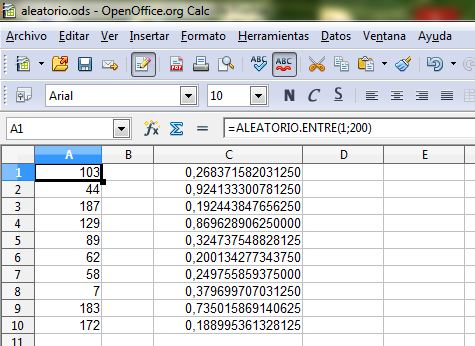
Licencia Creative Commons by-nc-sa
 |
Elabora una hoja de cálculo con el siguiente contenido:
- En la columna A debes obtener 10 números enteros aleatorios entre 1 y 500.
- En la columna C debes obtener 10 números aleatorios entre 0 y 1.
- Escribe en tu cuaderno los tres primeros números obtenidos en la columna A y los tres primeros de la columna C con tres cifras decimales.
Guarda la hoja de cálculo con el título aleatorios.calc y cierra el programa openoffice.calc.
Abre de nuevo la hoja de cálculo anterior y comprueba cómo han variado los números aleatorios generados en las columnas A y C.
Importante
Muestreos aleatorios:
- Muestreo aleatorio simple: se trata de obtener, mediante un método aleatorio, los individuos de la muestra entre los que forman la población. Este tipo de muestreo se realiza cuando los individuos de la población que vamos a estudiar tienen características parecidas. Así, por ejemplo, usaríamos este método en el estudio de la estatura media de los alumnos de 1º de E.S.O. de una determinada clase, ya que se supone que sus alturas serán parecidas.
- Muestreo estratificado aleatorio: se trata de dividir la población en grupos (llamados estratos) de características parecidas. De cada grupo se seleccionarán mediante un método aleatorio algunos individuos. El número de individuos obtenidos de cada grupo puede ser el mismo, (en cuyo caso se dice que se realiza mediante afijación igual), o proporcional al número de individuos que hay en total en dicho grupo con respecto al total de la población (en cuyo caso se llama afijación proporcional). Este tipo de muestreo nos permite obtener más información ya que, aparte de sacar resultados sobre el total de la población, nos da también información sobre los grupos (estratos) que lo forman. Siguiendo con el ejemplo anterior; si queremos estudiar la estatura media de los alumnos de E.S.O. de una población, podríamos tomar como estratos los cuatro grupos formados por los alumnos de 1º, 2º, 3º y 4º de E.S.O.
El número de individuos que hay que seleccionar en la afijación igual en cada estrato será n1=n2=n3=...= n/nº de estratos.
El número de individuos que hay que seleccionar en la afijación proporcional en cada estrato será n1=N1·n/N , n2=N2·n/N , n3=N3·n/N, ....
En ambos casos tendremos que n1 + n2 + n3 + ... = n

|
|
Libros. Imagen de Francisco Javier Martínez Adrados
en el banco de imágenes del ITE. Licencia Creative Commons by-nc-sa |
Se quiere realizar un estudio estadístico mediante muestreo estratificado aleatorio de cierto tipo de información de una biblioteca. Esta contiene un total de 2000 libros distribuidos de la siguiente forma:
- 800 libros de Literatura.
- 400 libros de Geografía e Historia.
- 500 libros de ciencia.
- 300 libros de otros contenidos.
Para el estudio se quiere tomar una muestra de 180 libros y considerar como estratos los grupos de libros anteriores.
Resuelve las siguientes cuestiones:
a) Valor de N (tamaño de la población) y de n (tamaño de la muestra).
b) Número de libros que hay que seleccionar para la muestra de cada uno de los distintos estratos si se realiza mediante afijación igual.
c) Número de libros que hay que seleccionar para la muestra de cada uno de los distintos estratos si se realiza mediante afijación proporcional.
 |
Se quiere realizar un estudio estadístico, mediante muestreo estratificado, del número de horas que ven la televisión los individuos de una población de 3000 personas. 500 son menores de edad, 1500 tienen entre 18 y 50 años y el resto son mayores de 50 años. Sabiendo que el número total de personas seleccionadas en la muestra es 150, indicar cuál es la opción correcta en cada una de las siguientes cuestiones.
El número de individuos de la población y de la muestra es:


