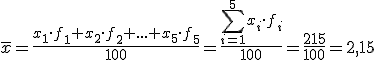4.2 Con tablas

|
|
|
Ya sabes calcular los parámetros centrales de un conjunto de datos. Pero, ¿te servirá lo aprendido en todos los casos? Si quieres saber cuál es el gasto mensual medio que tienes de leche en tu casa, no hay mucha dificultad. Basta hallar la media de los litros de leche que habéis consumido durante los doce meses de un año. Pero si fueses el gerente de una cadena comercial con miles de empleados y quisieras saber cuál es la edad media de tus empleados, sería más complicado
Si recuerdas el ejemplo de los sueldos de apartado anterior, había tres empleados que cobraban 950 euros. A la hora de hallar la media, podíamos sumar tres veces ese valor o calcular 950·3. En el caso de tres no parece muy interesante, pero si se repitiera el mismo sueldo 231 sería distinto: no costaría igual tener que sumar 231 veces una misma cantidad en lugar de multiplicarla por 231. Por es,o cuando tenemos muchos datos, los cálculos de los parámetros se realizan a través de la tabla de frecuencia.
Importante
El cálculo de los parámetros de centralización a través de las tablas de frecuencia se realiza de la siguiente forma:
Mediana: como los valores están ordenados en la tabla de frecuencias, el procedimiento consiste en calcular la frecuencia absoluta acumulada. Se divide el número total de datos recogidos (N) entre dos. El primer valor cuya frecuencia absoluta acumulada supera a esa cantidad, es el valor mediano. Esto es debido a que si escribiésemos todos los valores ordenados uno detrás de otro, la frecuencia acumulada nos indicaría hasta qué lugares llegaban cada uno de los distintos valores.
Si la mitad de N coincide exactamente con el valor de la frecuencia acumulada de un valor, estaríamos como en el mismo caso del apartado anterior cuando teníamos un número par de valores. En ese caso, la mediana es la semisuma de ese valor y el siguiente.
Media: en lugar de sumar cada valor todas las veces que aparezca, multiplicamos el valor de la variable por la cantidad de veces que aparece (frecuencia absoluta). La suma de todos esos valores la dividimos entre el número total de valores recogidos. Se aplicaría la fórmula siguiente:
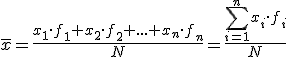
 |
Si en lugar de valores de una variable discreta, tuviésemos valores de una variable continua, el proceso es muy similar. En este caso, en lugar de moda se habla de intervalo modal y, de momento, en lugar de mediana hablaremos de intervalo mediano.
Para hallar la media, únicamente hay que tener en cuenta que se toma como valor xi de la variable el de la marca de clase.
| nº de televisores | nº de hogares |
| 0 | 6 |
| 1 | 30 |
| 2 | 28 |
| 3 | 21 |
| 4 | 9 |
| 5 | 6 |
En el estudio del número de televisores por familia de un barrio se ha recogido la información que se muestra en la tabla.
Calcula la moda, la mediana y la media de esos valores.
En el siguiente enlace a un documento OpenOffice.calc puedes ver el cálculo de la media de la actividad anterior. Observa como para totalizar las columnas, se utiliza la función SUMA.

|
| Espárragos.
Imagen del ITE en el banco de imágenes del ITE
Licencia Creative Commons by-nc-sa
|
Una empresa envasadora de espárragos blancos quiere estudiar la posibilidad de lanzar al mercado envases de dos tamaños. Uno para productos más grandes, lógicamente de mayor precio, y otro para los elementos más pequeños. Para ello hace un estudio aleatorio del tamaño de espárragos que va envasando, obteniendo los siguientes resultados:
|
Medida en cm. Intervalos |
Nº de espárragos fi |
| [7,9) | 25 |
| [9,11) | 172 |
| [11,13) | 311 |
| [13,15) | 413 |
| [15,17) | 79 |
Completa la tabla con la frecuencia acumulada, la marca de clase y los valores xi·fi. Después, calcula los parámetros de centralización y contesta a las siguientes preguntas:
a) El intervalo modal es [ , ).
b) El intervalo mediano es [ , ).
c) La media, redondeada a dos decimales, vale
.
Medias. Escena de José Ireno Fernánde Rubio en ITE
Licencia Creative Commons by-nc-sa |
Curiosidad
 |
Hemos comentado que la mediana y la media no tienen sentido en las variables cualitativas. No obstante, a veces, para poder sacar esa información incluso en datos no numéricos, lo que se hace es codificar las respuestas. Por ejemplo, a veces te habrás encontrado encuestas en las que, al preguntarte sobre cuál es tu grado de satisfacción con un determinado servicio, te habrán pedido que elijas un número del 1 al 5 (el 1 significa nada satisfecho y el 5 muy satisfecho).
De esa forma se evalúan los datos numéricos correspondientes y se pueden hallar todos los parámetros.

|
|
Pantalla de ordenador.
Imagen de Fco. Javier Martínez Adrados
en el banco de imágenes del ITE
Licencia Creative Commons by-nc-sa |
Una vez que has llegado a este punto, suponemos que ya dominas los parámetros de centralización. Debes recordar siempre que esos parámetros representan valores alrededor de los cuales se agrupan los datos recogidos en el estudio estadístico. La moda es donde hay más, la mediana es el punto medio exacto de los datos y la media equivale al centro de gravedad de la distribución de valores. Pero, como es lógico, con esos valores no es suficiente para tener toda la información sobre los datos.
Por si no te ha quedado clara la dificultad de utilizar sólo los parámetros estadísticos centrales imagina un ejemplo. Hemos preguntado a 15 personas sobre las veces que se conectan al día a Internet fuera de su trabajo y, tras estudiar las respuestas, nos ha salido una media de 3 veces al día, ¿es esa suficiente información? Posiblemente esa sola no nos sirva, ya que puede haber muchos casos. Por ejemplo, puede darse el caso de que prácticamente todos dediquen el mismo tiempo o que haya unos que dediquen muy poco tiempo y otros mucho.
Precisamente por esta dificultad es por lo que necesitaremos más parámetros estadísticos que vamos a desarrollar a continuación.