4.4 Posición

Gente haciendo cola. Imagen del ITE en el banco de imágenes del ITE

Licencia Creative Commons by-nc-sa

¿Has estado alguna vez en un importante museo, en un concierto de un artista de éxito o en unos grandes almacenes a principio de mes? Seguro que recordarás las largas colas. Donde las colas de espera están bien organizadas, nosotros hemos encontrado indicaciones como estas: primero un letrero que indicaba "a partir de aquí 30 minutos de espera", unos metros más adelante otro de "desde aquí 15 minutos" y así sucesivamente. Es una forma de compartimentar la cantidad de personas que esperan y el tiempo que se tardará en llegar a la entrada o ventanilla. Algo similar hacen los parámetros que vamos a ver a continuación.

Se llaman parámetros de posición aquellos que dividen a los datos obtenidos en partes proporcionales, de forma que cada parte tenga el mismo número de elementos. Para poder hacerlo necesitamos que los datos estén ordenados de menor a mayor. Los hay de tres tipos: cuartiles, deciles y percentiles, aunque vamos a desarrollar solo los cuartiles.

Importante

Se definen los cuartiles como los valores que dividen a la distribución de valores ordenados en cuatro partes iguales. Son los siguientes:

Q₁: primer cuartil. Tiene el 25% de los datos detrás de él y el 75% delante.
Me: segundo cuartil .Coincide con la mediana. Tiene el 50% de los datos delante y el otro 50% detrás de él.
Q₃: deja detrás de él el 75% de la distribución y delante el 25%.

Se define el recorrido intercuartílico a la diferencia entre el tercer y el primer cuartil. Dentro de este intervalo se encuentra el 50% de la distribución. Un estudio conjunto del recorrido y del recorrido intercuartílico nos da información sobre la dispersión de la muestra. Si el recorrido general es grande pero el intercuartílico pequeño, eso indica que hay valores extremos. Si ambos son grandes, los datos son dispersos. Si ambos son pequeños, los datos están muy agrupados respecto a los valores centrales.

Para calcular los cuartiles basta generalizar el cálculo de la mediana que ya habíamos visto. Se halla 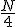y el primer valor cuya frecuencia absoluta acumulada supera ese valor es Q₁. Para Q₃ debemos hallar 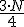y seleccionar aquel valor cuya frecuencia acumulada supera esa cantidad. Hay que recordar (como en la mediana) que si un valor tiene como frecuencia acumulada exactamente ese valor, se halla la media aritmética con el valor siguiente.

Aprende a hacerlo

Veamos en primer lugar el cálculo de los cuartiles cuando los datos no están agrupados en intervalos.

Pastilla. Imagen del ITE en el banco de imágenes del ITE

Licencia Creative Commons by-nc-sa

Para realizar un estudio sobre el gasto farmacéutico en la sanidad pública, le encargan a Mercedes que haga un estudio sobre el número de medicamentos por paciente que se receta en una determinada consulta a lo largo de una semana. Tras estudiar los datos, Mercedes obtiene la siguiente tabla.

nº de medicamentos (x_i)	1	2	3	4	5	6	7	8	9	10
nº de pacientes (f_i)	12	24	15	13	9	6	2	1	1	1

Calcula los cuartiles de esa distribución.

Solucion:

Necesitamos la frecuencia acumulada y dividir N en cuartos, para lo cual en primer lugar procedemos a completar la tabla.

x_i	f_i	F_i
1	12	12
2	24	36
3	15	51
4	13	64
5	9	73
6	6	79
7	2	81
8	1	82
9	1	83
10	1	84
N=	84

Como N=84, N/4=84/4=21

El primer cuartil, por tanto, se alcanza para x=2 (buscamos el primer valor de la frecuencia absoluta acumulada que supera o iguala a 21), Q₁ = 2

El segundo cuartil (mediana) es el valor para el que la frecuencia absoluta acumulada supera o iguala a N/2=84/2=41 , luego M_e = 3

El tercer cuartil es el valor para el que la frecuencia absoluta acumulada supera o iguala a N=3·84/4=63 , y por tanto Q₃ = 4

Ejemplo o ejercicio resuelto

Espárragos. Imagen del ITE en el banco de imágenes del ITE

Licencia Creative Commons by-nc-sa

Considera la distribución del ejemplo de las medidas de los espárragos que estamos trabajando en este tema.

Medida en cm, intervalos	Nº de espárragos f_i
[7,9)	25
[9,11)	172
[11,13)	311
[13,15)	413
[15,17]	79

Halla los tres cuartiles de esa distribución.

La tabla con las frecuencias absolutas acumuladas es:

Medida en cm, intervalos	Nº de espárragos f_i	F_i
[7,9)	25	25
[9,11)	172	197
[11,13)	311	508
[13,15)	413	921
[15,17)	79	1000
N=	1000

Ve pulsando sobre la ventana y observa los pasos que debemos dar.

Procedemos de forma análoga al ejercicio anterior con la diferencia de que ahora tendremos que realizar las proporciones necesarias para calcular, dentro de los intervalo,s los valores que se corresponden a los distintos cuartiles.

Calculamos primero los valores N/4, N/2 y 3N/4. Estos valores son N/4=1000/4=250, N/2=1000/2=500 y 3N/4=750.

Q1 (primer cuartil)

Buscamos el primer intervalo para el que se alcanza el valor N/4=250 en la columna F_i.Vemos que es el intervalo [11,13) cuya frecuencia acumulada es 311. Por tanto, el valor de Q₁ estará comprendido entre 11 y 13. Para calcular dicho valor realizamos la siguiente proporción:

A la frecuencia absoluta 311 le corresponde una diferencia de 13-11=2. Por tanto, a 250-197 =53 le corresponderá una amplitud de x.

Planteamos la regla de tres

311	-------	2
53	-------	x

de donde obtenemos que x=2·53/311=0,34, por tanto Q₁ = 11+0,34 = 11,34 cm

M_e (segundo cuartil)

Buscamos el primer intervalo para el que se alcanza el valor N/2=500 en la columna F_i. Vemos que es el intervalo [11,13) cuya frecuencia acumulada es 311. Por tanto, el valor de M_e estará comprendido entre 11 y 13. Para calcular dicho valor realizamos la siguiente proporción:

A la frecuencia absoluta 311 le corresponde una diferencia de 13-11=2, por tanto a 500-197 =303 le corresponderá una amplitud de x.

Planteamos la regla de tres

311	-------	2
303	-------	x

de donde obtenemos que x=2·303/311=1,95, por tanto Me = 11+1,95 = 12,95 cm

Q3 (tercer cuartil)

Buscamos el primer intervalo para el que se alcanza el valor 3N/4=750 en la columna F_i. Vemos que es el intervalo [13,15), cuya frecuencia acumulada es 413. Por tanto, el valor de Q₃ estará comprendido entre 13 y 15. Para calcular dicho valor realizamos la siguiente proporción:

A la frecuencia absoluta 413 le corresponde una diferencia de 15-13=2. Por, tanto a 750-508 =242 le corresponderá una amplitud de x.

Planteamos la regla de tres

413	-------	2
242	-------	x

de donde obtenemos que x=2·242/413=1,17, por tanto Q₂ = 13+1,17 = 14,17 cm .

En resumen tenemos que: Q₁ = 11,34 cm , Me = 12,95 cm y Q₂ = 14,17 cm

Solucion:

La tabla con las frecuencias absolutas acumuladas es:

Medida en cm, intervalos	Nº de espárragos f_i	F_i
[7,9)	25	25
[9,11)	172	197
[11,13)	311	508
[13,15)	413	921
[15,17)	79	1000
N=	1000

Ve pulsando sobre la ventana y observa los pasos que debemos dar.

Calculamos primero los valores N/4, N/2 y 3N/4. Estos valores son N/4=1000/4=250, N/2=1000/2=500 y 3N/4=750.

Q1 (primer cuartil)

A la frecuencia absoluta 311 le corresponde una diferencia de 13-11=2. Por tanto, a 250-197 =53 le corresponderá una amplitud de x.

Planteamos la regla de tres

311	-------	2
53	-------	x

de donde obtenemos que x=2·53/311=0,34, por tanto Q₁ = 11+0,34 = 11,34 cm

M_e (segundo cuartil)

A la frecuencia absoluta 311 le corresponde una diferencia de 13-11=2, por tanto a 500-197 =303 le corresponderá una amplitud de x.

Planteamos la regla de tres

311	-------	2
303	-------	x

de donde obtenemos que x=2·303/311=1,95, por tanto Me = 11+1,95 = 12,95 cm

Q3 (tercer cuartil)

A la frecuencia absoluta 413 le corresponde una diferencia de 15-13=2. Por, tanto a 750-508 =242 le corresponderá una amplitud de x.

Planteamos la regla de tres

413	-------	2
242	-------	x

de donde obtenemos que x=2·242/413=1,17, por tanto Q₂ = 13+1,17 = 14,17 cm .

En resumen tenemos que: Q₁ = 11,34 cm , Me = 12,95 cm y Q₂ = 14,17 cm

En la siguiente escena puedes realizar algunos ejercicios de cálculo de cuartiles. Puedes practicar varios ejemplos tanto para variables discretas como continuas. Utiliza el botón "Discreta/Continua" para seleccionar el tipo y pulsa el botón "Genera" para realizar otro ejercicio. Deberás completar la tabla en tu cuaderno y realizar los distintos cálculos.

Si en el ejemplo que estés resolviendo pulsas en ayuda, te indicará otra forma de hallar los cuartiles. Consiste en dibujar una línea de colores en la que cada color tenga de longitud la frecuencia absoluta de cada resultado y, después, dividir esa línea en cuatro partes.