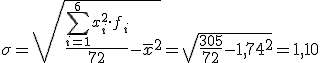4.3 Dispersión
 |
|
Nectarinas.
Imagen del ITE en el banco de imágenes del ITE
Licencia Creative Commons by-nc-sa
|
Se llaman parámetros de dispersión a una serie de valores que indican lo concentrados o separados están los datos entre sí y respecto a la media.
Importante
Se llama recorrido o amplitud del rango a la diferencia entre el valor más pequeño y el más grande que se ha recogido. Nos da una primera idea de si los datos están agrupados o están muy separados, al menos en lo que respecta a los valores menores y mayores.
|
nº de hijos xi |
nº de familias fi |
| 0 | 6 |
| 1 | 30 |
| 2 | 20 |
| 3 | 10 |
| 4 | 5 |
| 5 | 1 |
En el estudio del número de hijos por familia de un barrio se ha recogido la información que se muestra en la tabla.
| xi | fi |
| [5,6) | 30 |
| [6,7) |
50 |
| [7,8) | 40 |
| [8,9) | 20 |
En el estudio de las ciruelas de una determinada producción se han obtenido los datos del calibre en cm que aparecen en la tabla. El estudio se ha hecho a partir de una muestra de 140 piezas. ¿Cuál es el recorrido o amplitud de rango de los calibres de las piezas de ciruelas estudiadas?
Importante
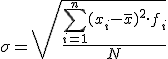
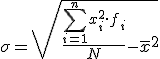
La segunda expresión es la que normalmente se suele utilizar ya que, si nos basamos en la tabla de frecuencias, basta añadir una nueva columna correspondiente a xi2·fi y totalizarla.
La desviación típica nos da información sobre cómo se desvían los datos respecto a la media, de forma que cuanto mayor sea más alejados están los datos de ella.
Al cuadrado de la desviación típica se le llama varianza, varianza = σ2, que es otro parámetro de dispersión que también se suele utilizar en estadística.

|
|
Las tres hermanas: la boda de Asunción.
Imagen de Nuria Pérez Cuadrado en el banco de imágenes del ITE
Licencia Creative Commons by-nc-sa
|
Vamos a retomar el ejercicio del número de hijos por familia del barrio. Teníamos la tabla siguiente:
|
nº de hijos xi |
nº de familias fi |
| 0 | 6 |
| 1 | 30 |
| 2 | 20 |
| 3 | 10 |
| 4 | 5 |
| 5 | 1 |
Vamos a calcular su media y su varianza.
En el siguiente enlace a un documento OpenOffice.calc puedes ver el cálculo de la media y de la desviación típica de la actividad anterior. Observa que hemos introducido dos nuevas funciones:
-
REDONDEAR(Número a redondear;nº de decimales): redondea un número con el número de cifras decimales que se indique. Por ejemplo, REDONDEAR(5,456;2) redondeará el número 5,456 a dos cifras decimales y por tanto nos devolverá el valor 5,46.
- RAÍZ(número) , devuelve la raíz cuadrada del número que se especifique.
Desviación típica. Escena de José Ireno Fernánde Rubio en ITE
Licencia Creative Commons by-nc-sa |
 |
|
Carlos V con perro, de Tiziano.
Imagen del ITE en el banco de imágenes del ITE
Licencia Creative Commons by-nc-sa
|
Mediante la siguiente tarea queremos que realices un estudio del número de animales que tienen en su casa distintas familias de tu entorno más cercano: tus propios familiares, amigos y algunos de tus compañeros. Para ello debes realizar las siguientes actividades:
1) Selecciona 12 personas que no vivan en la misma casa y pregúntales cuántos animales tienen en casa.
2) Recoge la información en una tabla de frecuencias creándola con OpenOffice.calc.
3) Añade a la tabla las columnas necesarias para poder calcular la media y la desviación típica.
4) Calcula, utilizando dos cifras decimales, la media y la desviación típica.
5) Representa en un diagrama de barras o de sectores la distribución del número de animales.
6) Analiza los resultados obtenidos, indicando si existe o no una gran dispersión de los datos.
Una vez que hayamos terminado el proceso, guarda el archivo en tu carpeta personal y realiza una entrada en el blog. El titulo de la entrada estará formado por dos partes, la primera será la inicial de tu nombre y tu primer apellido y la segunda será animales.
Utiliza dicho documento para realizar una exposición a tus compañeros y explicarles los resultados obtenidos del estudio.

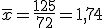 .
.