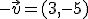1.1 Coordenadas y operaciones
Anota en tu cuaderno las siguientes definiciones y ejercicios de este apartado.
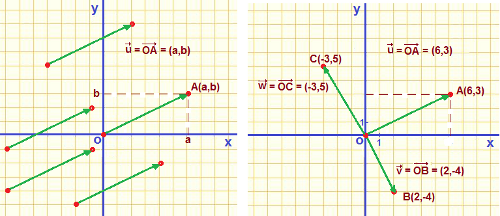
Si representamos un vector en un sistema de coordenadas cartesianas de tal forma que su origen se haga coincidir con el del sistema, podemos asignarle las coordenadas del extremo del vector. A estas coordenadas también se les llama componentes del vector.
 |
|
|
Las componentes del vector de extremos A (a,b) y B (a',b'); las podemos obtener restando a las coordenadas del punto B las del A.
Aprende a hacerlo
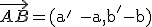
Dados los puntos:
- A (2,4)
- B (1,5)
- C (0,-2)
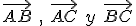
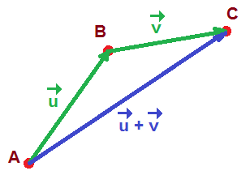
Suma de dos vectores
 |
|
Suma de vectores. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa |
Geométricamente se realiza haciendo coincidir el extremo del primero con el origen del segundo, siendo el vector suma el obtenido al unir el origen del primero con el extremo del segundo.
Si los vectores vienen dados por sus componentes, basta sumarlas:
Aprende a hacerlo
 |
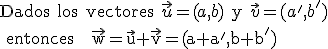
Dados los vectores:
 |
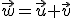
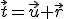
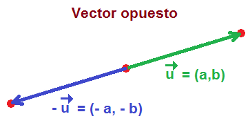Es aquel que tiene el mismo módulo, dirección y sentido opuesto. Sus componentes son las del vector dado cambiadas de signo.
Aprende a hacerlo
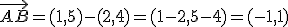
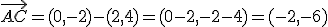
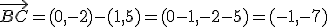
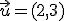
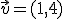
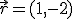
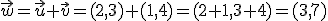
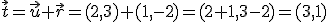
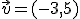
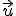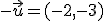
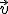Dados los vectores:
