2.2. Simetrías

Icono de iDevice

Importante

Simetría central

Se definine simetría central respecto a un punto O a la transformación que hace corresponder a cada punto P del plano otro punto P' tal que los vectores 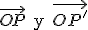son opuestos entre sí, es decir . 


En la siguiente escena se representa la simetría central de un objeto real.

  • Observa cómo el vector que une los puntos O y P es opuesto al que une O y P' (su homólogo), para ello puedes mover el vector w.
  • Mueve el punto P para mover la oca y observar cómo se obtiene su simétrica.
  • Mueve los puntos O para modificar el centro de simetría.
Please install Java 1.4 (or later) to use this page.

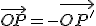Simetría cental de una oca. Escena de Arturo Mandly Manso elaborado con Geogebra

Licencia Creative Commons by-nc-sa


Icono de iDevice

Importante
Ave Fénix. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa

 

 

Simetría axial 

Se define simetría axial respecto a una recta r (llamada eje de simetría) a la transformación que hace corresponder a todo punto P del plano otro punto P'; de tal forma que, r  es la mediatriz del segmento PP', es decir que la distancia de P y P' a la recta r es la misma.


 

 

 

 


En la siguiente animación puedes ver el procedimiento para obtener el simétrico de un punto respecto a una recta.

Representación geométrica de la simetría axial.
Animación de José Ángel López Mateos en el banco de imágenes del ITE.
Licencia Creative Commons by-nc-sa

En la siguiente escena se representa la simetría axial de un objeto real.

  • Observa cómo los puntos simétricos están a la misma distancia del eje de simetría.
  • Mueve el punto P para mover la oca y observar cómo se obtiene su simétrica.
  • Mueve los puntos A y B para modificar el eje de simetría.
  • ¿Dónde tendría que estar situado el punto P para que coincida con su homólogo P'?.
  • ¿Se puede conseguir que las dos ocas coincidan?
Please install Java 1.4 (or later) to use this page.

Simetría axial de una oca. Escena de Arturo Mandly Manso elaborado con Geogebra

Licencia Creative Commons by-nc-sa


Icono de iDevice Tarea

Traza en tu cuaderno un sistema de coordenadas cartesianas y realiza las siguientes actividades:

a) Dibuja la letra M con cierta inclinación  en el tercer cuadrante con trazos rectos y sus extremos en puntos de coordenadas enteras.

b) Escribe las coordenadas de cada uno de los puntos extremos que determinan dicha letra.

c) Dibuja la imagen simétrica de dicha letra respecto a la bisectriz del segundo y cuarto cuadrante.

d) Anota las coordenadas de los puntos simétricos que te han permitido obtener la imagen simétrica.

 

 

Icono de iDevice de pregunta Comprueba lo aprendido
¿Cuál de los siguientes puntos es el simétrico del punto A(-3,4) respecto al eje OY?
    
a) (-3,-4)
b) (3,4)
c) (4,-3)

¿Cuál de los siguientes puntos es el simétrico del punto B(3,-2) respecto al eje OX?
    
a) (-3,2)
b) (-3,-2)
c) (3,2)

En el siguiente enlace a un vídeo puedes ver la generación de figuras simétricas a partir de espejos. 

 

Icono de iDevice

Curiosidad
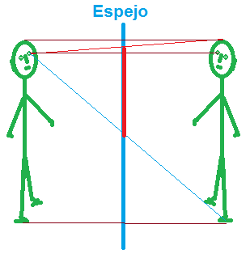
Altura mínima de un espejo. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa

 

La altura mínima que debe tener un espejo para que una persona se vea totalmente en él debe ser la mitad de su altura.


Matemáticas 3º E.S.O. CeDeC