2.1. Traslaciones
Importante

|
|
|
Traslación
Se define traslación producida por un vector libre 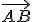 a la transformación que hace corresponder a todo punto P del plano otro punto P' de tal forma que
a la transformación que hace corresponder a todo punto P del plano otro punto P' de tal forma que 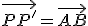
Para obtener las coordenadas del punto P' basta con sumarle a las de P las componentes del vector 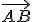
|
Traslación. Escena de Ricardo Alonso Liarte en Descartes
Licencia Creative Commons by-nc-sa |
En la siguiente escena puedes obtener la traslación de un objeto real.
- Modifica el vector como en la escena anterior y observa cómo se transforma la oca.
- Coloca el origen del vector encima de un punto de la oca y comprueba que el extremo está en el mismo punto de la otra oca.
Traslación de una oca. Escena de Arturo Mandly Manso elaborado con Geogebra
Licencia Creative Commons by-nc-sa
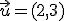 determinar las coordenadas de los puntos obtenidos por traslación mediante dicho vector de los siguientes puntos:
determinar las coordenadas de los puntos obtenidos por traslación mediante dicho vector de los siguientes puntos:
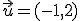
 |
a) Dibuja la letra E en el segundo cuadrante con trazos rectos y sus extremos en puntos de coordenadas enteras.
b) Escribe las coordenadas de cada uno de los puntos extremos que determinan dicha letra.
c) Calcula las coordenadas de los puntos obtenidos al aplicarles una traslación de vector 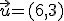
d) Dibuja los puntos del apartado anterior.
e) ¿Qué se obtiene al unir dichos puntos de la misma forma que lo están en los originales?
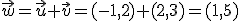 , aplicando dicho vector al punto M(-1,-2) obtenemos (-1+1,-2+5)=(0,3)
, aplicando dicho vector al punto M(-1,-2) obtenemos (-1+1,-2+5)=(0,3)
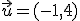 ?
?

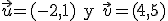 ?
?
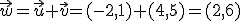 , y por tanto las coordenadas del homólogo serán (1+2,-1+6)=(3,5)
, y por tanto las coordenadas del homólogo serán (1+2,-1+6)=(3,5)