1.3. Monomios y polinomios
 |
|
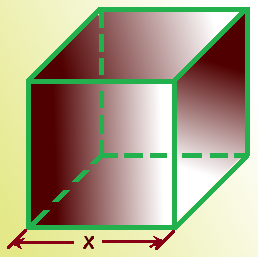
Cubo. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa |
Del cubo de la figura podemos expresar su volumen y su superficie total en función de la medida de sus aristas (x):
Volumen V(x) = x3
Superficie total S(x) = 6x2
Estas fórmulas forman parte de las expresiones algebraicas más sencillas llamadas monomios en las cuales el valor particular se obtiene cuando sustituimos la letra x por un valor concreto. Así por ejemplo si x = 4 cm, tendremos que V = 43 = 64 cm3 y S = 6·42 = 96 cm2.
A partir de estas expresiones, se pueden construir otras también sencillas llamadas polinomios y a partir de ellos a su vez otras más complejas.
Los monomios están formados por una parte numérica y por otra literal que puede contener una o varias letras que denominamos variables.
Importante
Escribe en tu cuaderno las siguientes definiciones y ejemplos:
Monomios: son las expresiones más sencillas y están formadas por una parte numérica llamada coeficiente (cuando es 1 se suprime) y una parte literal formada por una letra elevada a un exponente natural (o el producto de varias de estas potencias). De esta forma, las dos expresiones anteriores se corresponden a monomios.
Así por ejemplo, en el monomio 15x2 , el coeficiente es 15 y la parte literal es x2 .
En el monomio x3, el coeficiente es 1 y la parte literal es x3 .
También se considerará como un monomio a aquel que sólo tiene parte numérica. De esta forma, 8 por ejemplo, sería un monomio. Cuando forma parte de otra expresión más compleja, como por ejemplo 2x + 8 , diremos que es el término independiente.
Dos monomios son semejantes si tienen la misma parte literal:
- 8x2 , -5x2 , x2 son monomios semejantes (todos tienen la misma parte literal x2)
- 3xy4, -2xy4 son monomios semejantes (todos tienen la misma parte literal xy4 )
- x2 y 7x3 , no son semejantes ya que en el primero su parte literal es x2 y en el otro x3 (son diferentes).
 |
Definiciones
- Un polinomio es una "suma de monomios". Cada uno de los sumandos que aparecen se denomina término del polinomio y cada uno es un monomio. El grado del polinomio es el grado mayor de los monomios que lo forman.
- El valor numérico de un polinomio para un determinado número, es el número que se obtiene sustituyendo x por dicho número. Ejemplo: si P(x) = 2x3-5x+4 , P(2) = 2·23-5·2+4 = 2·8-10+4 = 10.
- El número a es raíz o cero de un polinomio P(x) si P(a)=0.
Ejemplos:
1. P(x) = x2-3x+2 tiene por raíces x=1 y x=2.
2. P(x) = x2-2x+1 = 0 tiene por única raíz x = 1, pues x2-2x+1 = (x-1)2 (en este caso se dice que la raíz es doble).
3. P(x)= x2+1 = 0 no tiene ninguna raíz real, pues el cuadrado de todo número real es positivo (así x2+1>0).
