5.1. Resolución general

Importante

Una ecuación de segundo grado es una ecuación que tras simplificarla y pasar todos los términos a un lado queda de la forma:

ax² + bx + c = 0 (siendo a≠0)

Para resolverlas se usa la fórmula

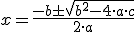
En la siguiente escena puedes ver distintos ejemplos de ecuaciones de segundo grado resueltas. Observa cómo se han resuelto.

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Ecuaciones de segundo grado Escena del ITE en Descartes

Licencia Creative Commons by-nc-sa

Pulsa en el control para ver distintos ejemplos.

Observa que siempre "a" es el número que multiplica a x²; "b" el que multiplica a x y "c" el número sin x, teniendo en cuenta en todos los casos los signos.

En la red

En el siguiente enlace vas a resolver ecuaciones de segundo grado.

Pulsa sobre el botón "ejercicio", resuelve la ecuación que aparece y, antes de introducir los valores en las casillas para comprobar, elige la opción que se ajuste a tu caso en la ventana "Tipo de solución".

Seleccionada esta, introduce los valores de las soluciones y pulsa sobre el botón "solución" para comprobar si lo has hecho bien.

Realiza 8 ejercicios. Si tienes menos de 5 puntos, repítelo.

Importante

Como puedes ver, a veces hay dos soluciones, a veces una y otras no hay solución.

Esto depende del número que nos quede dentro de la raíz, o sea, del valor de la expresión

"b² - 4·a·c",

que se llama discriminante:

Si es positivo, hay dos soluciones.

Si es cero, hay una única solución.

Si es negativo, no existe solución real; pues como sabes, la raíz cuadrada de un número negativo no existe.

En la red

En el siguiente enlace puedes realizar ejercicios de aplicación del discriminante sin necesidad de resolver la ecuación de segundo grado. Realiza cinco ejercicios de este tipo y cópialos en tu cuaderno.

Aprende a hacerlo

Vamos a resolver un ejercicio típico de aplicación de los distintos valores que puede tomar el discriminante de una ecuación de segundo grado. Como verás, aparte de la incógnita de la ecuación aparece otra letra, en este caso m, que se llama parámetro y que hace que las soluciones cambien dependiendo del valor que tome.

Dada la ecuación x²+2x+m-1=0

a) ¿Cuál es la expresión que nos permite determinar su discrimintante?

b) ¿Qué valor debe tomar m para que la ecuación tenga sus dos soluciones iguales?

c) ¿Tiene solución real la ecuación si m=3?

d) ¿Cuántas soluciones tiene la ecuación si m=1?

Solucion:

a) El discriminante es igual a 2²-4·1·(m-1) = 4 - 4m + 4 = 8 - 4m

b) Para que la ecuación tenga sus dos soluciones iguales el discriminante debe ser nulo, por tanto:

8-4m = 0 => -4m = - 8 => 4m = 8 => m = 8/4 = 2 . Solución el valor de m debe ser 2.

c) Para m=3 el discriminante toma el valor 8-4·3 = 8 - 12 = -4 . Como el resultado es negativo podemos afirmar que la ecuación no tiene solución real.

c) Para m=1 el discriminante toma el valor 8-4·1= 8 - 4 = 4 . Como el resultado es mayor que cero podemos afirmar que la ecuación tiene dos soluciones diferentes.

Comprueba lo aprendido

Dada la ecuación x²+4x+2m-1=0 ¿cuál de los siguientes valores de m hace que las dos soluciones de la ecuación sean iguales?

a) 2

b) 0

c) 5/2

Solucion:

Incorrecto Incorrecto. Repasa los cálculos. Observa que el discriminante para m=2 es 4 y dicho valor no es 0.
Incorrecto Incorrecto. Repasa los cálculos. Observa que el discriminante para m=0 es 20 y dicho valor no es 0.
Opción correcta
Correcto. El discriminante es igual a 4²-4·(2m-1)=16-8m+4=20-8m

Igualando a cero el discriminante => 20 - 8m = 0, cuay solución es m = 5/2.

Curiosidad

Las soluciones de las ecuaciones de segundo grado tienen una seríe de propiedades relacionadas con sus coeficientes a, b y c.

En el siguiente enlace puedes estudiarlas y realizar algunos ejercicios basados en ellas.

Matemáticas 3º E.S.O. CeDeC

Este obra está bajo una licencia de Creative Commons Reconocimiento-CompartirIgual 3.0 España.

« Anterior | Siguiente »