5.2. Ecuaciones incompletas
 |
|
Galería con una exposición fotográfica. Imagen de .SantiMB. en Flickr
Licencia Creative Commons by-nc-sa. |
Pero... ¿y si falta alguien? ¿Qué hacemos? ¿Cómo lo resolvemos?
En numerosas ocasiones, las ecuaciones de segundo grado no quedan completas, sino que falta algún término. Sin ir más lejos, el ejemplo con el que empezamos el apartado anterior, ¿recuerdas?, el del expositor que quería comprar Juan que ocupara 6 metros cuadrados, nos daba como ecuación:
x2 = 6 ,
y si lo expresamos como las ecuaciones generales, nos quedaría:
x2 - 6 = 0,
o sea, una ecuación en la que falta el término con x; falta b.
Estos casos podríamos resolverlos utilizando la fórmula y dándole al término que faltara el valor 0.
Por ejemplo, en la ecuación que acabamos de poner,
x2 - 6 = 0,
si usáramos la fórmula tendríamos que a = 1, b = 0, pues no hay término con x y c = -6. Sustituyendo nos quedaría:
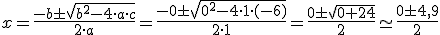
Luego tendríamos que una solución es 4,9/2 = 2,45 y la otra - 4,9/2 = -2,45; aunque en el contexto de nuestro problema, como x era la longitud del lado del expositor, la única solución válida sería 2,45 metros.
Pero seguro que estás pensando, ¿y para qué hace todo esto? ¡Si se puede hacer mucho más fácil! ¡Si sólo hay que hacer la raíz cuadrada de 6!, ¿verdad?
Importante
- Si falta el término en x, despejar x en la ecuación.
- Si falta el término sin x, sacar factor común x en el miembro de la izquierda y aplicar que si el producto es cero, alguno de los factores ha de ser cero.
En las siguientes escenas puedes ver cómo se resuelven estos ejercicios.
Ecuaciones de segundo grado incompletas Escenas del ITE en Descartes.
Licencia Creative Commons by-nc-sa
Observa que en la primera despejamos primero x2 y después hacemos la raíz cuadrada obteniendo las dos soluciones, una positiva y otra negativa.
En la segunda sacamos factor común x, y como el producto ha de ser cero, una solución es x= 0 y la otra sale de igualar el paréntesis a 0, pues para que el producto de dos cosas sea cero, al menos una de ellas tendrá que ser cero.
En la escena, aparecen ecuaciones incompletas de los dos tipos. Igual que antes, pulsa sobre el botón "EJERCICIO", selecciona el tipo de soluciones que tiene la ecuación que ha aparecido, introduce los valores obtenidos y finalmente pulsa sobre la "SOLUCIÓN" para comprobar si la solución es correcta.
Ecuaciones de segundo grado Escena de Miguel Ángel Cabezón Ochoa en Descartes.
Licencia Creative Commons by-nc-sa
Realiza 10 ejercicios. Si la nota es inferior a 5, repítelos.