2.1. Transformación de expresiones algebraicas
 |
Suma y resta: para sumar o restar monomios deben ser semejantes. Se suman o restan los coeficientes de cada monomio como resultado de sacar como factor común la parte literal.
Por ejemplo:
- 6 x2 + 3 x2 = 9 x2
- (-3 x4)-(-2 x4) = -3 x4 + 2 x4 = - x4
Producto: para multiplicar dos monomios se multiplican los coeficientes entre sí y se suman los grados (no es necesario que sean semejantes):
- 6 x2 · 3 x5 = 18 x7
- 2 x · 4 x5 = 8 x1+5 = 8 x6
- 2 x3(-3 x4) = - 6 x7
Cociente: para dividir dos monomios se dividen los coeficientes entre sí y se restan los grados (el resultado puede que no sea un monomio):
- 6 x7 : 3 x5 = 2 x7-5 = 2 x2
- 8 x7 : (-2 x) = -4 x7-1 = -4 x6
Potencia: la potencia de un monomio se obtiene elevando el coeficiente al exponente y multiplicando el grado del monomio por el exponente de la potencia:
- (2 x2)3 = 23 x2·3 = 8 x6
- (-2 x2)3 =(- 2)3 x2·3 =-8 x6
En la red

|
Si deseas ampliar la información sobre monomios, puedes visitar el siguiente enlace.
|

|
Visita el siguiente enlace para saber sobre monomios y operaciones. |
Al igual que con los monomios, se puede operar con polinomios de forma muy parecida.
Observa cuidadosamente las siguientes operaciones y anótalas en tu cuaderno:
Suma y resta: para sumar o restar dos polinomios se suman o restan entre sí los coeficientes de los monomios semejantes:
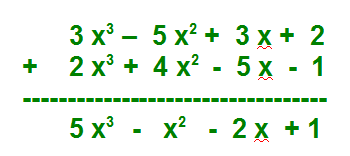
Producto: para multiplicar dos polinomios se multiplican todos y cada uno de los monomios del primero por todos y cada uno de los monomios del segundo, agrupando a continuación los monomios semejantes:
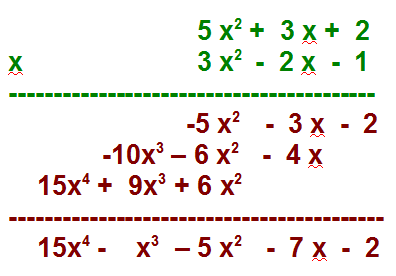
El producto también se puede realizar aplicando la multiplicación término a término y luego simplificando los términos del mismo grado:
| (2x +3)(2x-4) = 4x2 -8x + 6x - 12 = 4x2 -2x - 12 |
| (2x-3)(x2-2)= 2x3-4x-3x2+6 = 2x3 - 3x2 - 4x + 6 |
Cociente: para dividir dos polinomios, el grado del dividendo debe ser mayor o igual que el grado del divisor. Colocamos el polinomio dividendo completo; de forma que si falta algún término, se coloca un 0 en su lugar. Se dividen los términos principales de ambos polinomios, obteniéndose el primer monomio del cociente. Se multiplica ese monomio por el divisor y se resta del dividendo, con lo que el grado del dividendo disminuye. Se repite el proceso mientras que el grado del dividendo sea mayor o igual que el del divisor. Al final, obtenemos el polinomio cociente y el resto, que deberá tener grado menor que el divisor.
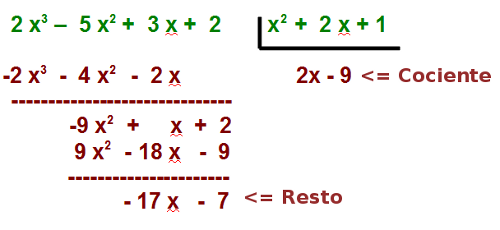
Dados los polinomios:
- P(x) = 2x2 - 5x + 3
- Q(x) = x2 + 3x - 2
Calcular:
a) P(x) + Q(x) =
b) 2 P(x)-3 Q(x) =
Calcular:
a) (2x-1) · P(x) =
b) (3x-2) · Q(x) =