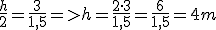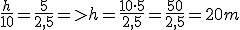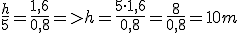2.1. Con espejos, sombras,...

Medida de alturas mediante espejos

Un método sencillo de cálculo de alturas se basa en la utilización de un pequeño espejo en el que se ve reflejado el punto más alto del objeto del que queremos determinar su altura. Las reflexiones nos permiten formar dos triángulos semejantes, tal y como puedes observar en la siguiente escena.

El material que se necesita por tanto es:

* Cinta métrica

* Espejo pequeño

* Palo de una longitud de por ejemplo 80 cm de largo o simplemente utilizamos nuestro propio cuerpo.

* Papel, lápiz y calculadora.

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Medición de alturas con espejos Escena de Miguel Martín Cano en Descartes

Licencia Creative Commons by-nc-sa


Icono de iDevice Tarea
Actividad para realizar por todo el grupo de la clase

 

Determinar, mediante el método, del espejo la altura del aula. Una vez terminada realizar las siguientes tareas:

  • Haz en tu cuaderno un dibujo que nos muestre el procedimiento empleado.
  • Anota las medidas directas y los cálculos que habéis realizado.
  • Reflexionar sobre los posibles errores que se pueden cometer en este procedimiento.

¿Te atreves a hacer un vídeo?

Realizad un vídeo con el procedimiento que habéis seguido para medir la altura del aula mediante el método del espejo comentando los pasos seguidos.

 
Medida de alturas mediante las sombras

Como sabemos; podemos considerar a los rayos solares paralelos, cuando inciden sobre; la Tierra debido a la gran distancia a la que se encuentra el Sol. Por tanto los ángulos que formarán dichos rayos de luz con el suelo en distancias próximas podemos considerarlos iguales.

El método para calcular la altura de un objeto se basa en esta propiedad que nos permite obtener dos triángulos rectángulos semejantes entre sí, siendo uno de ellos el que tiene por altura la del objeto a medir y de base su sombra proyectada, mientras que el otro triángulo lo obtenemos, por ejemplo, con un palo del que sabemos su altura y su sombra.

Vamos a aplicar este método al cálculo de la altura del torreón de la siguiente imagen.

 

Torreón y Thales trazos. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa

 

Como podemos observar los dos triángulos son semejantes y por tanto podemos aplicar el teorema de Thales.

Si llamamos h a la altura a determinar y s a la longitud de la parte sombreada, y llamamos h' a la altura del palo y s' a la longitud de su sombra, tendremos:

 

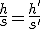  despejando tendremos: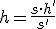   

Expresión que nos permitirá calcular la altura del torreón.

En la siguiente escena puedes practicar el método de las sombras para calcular la altura de un árbol.

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Cómo medir alturas inaccesibles Escena de Consolación Ruiz Gil Javier de la Escosura Caballero en Descartes

Licencia Creative Commons by-nc-sa


Icono de iDevice de pregunta Comprueba lo aprendido
Una farola proyecta una sombra de 2 m. En el mismo momento una estatua de 3 m de altura proyecta una sombra de 1,5 m. La farola tiene de altura:
    
a) 3,5 m
b) 4,2 m
c) 4 m

El campanario de una iglesia proyecta una sombra de 10 m. En el mismo momento una farola de 5 m de altura proyecta una sombra de 2,5 m. La altura del campanario es de:
    
a) 20 m
b) 22,5 m
c) 19 m

Una persona cuya distancia de sus ojos al suelo es de 1,6 m observa a través de un espejo colocado a 0,8 m de él el alero de un tejado que está sobre una pared que dista 5 m del espejo. La altura a la que está el alero del tejado es:
    
a) 12 m
b) 10 m
c) 11 m

Icono de iDevice

Curiosidad

El matemático griego Eratóstenes, basándose en las sombras proyectadas por los rayos de luz, ideó un procedimiento que le permitió calcular el radio de la Tierra.

Puedes visitar el siguiente vídeo para ver el procedimiento que empleó Eratóstenes.

El método que se presenta en la siguiente escena lo puedes generalizar para calcular la distancia entre dos objetos.

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Distancia entre dos árboles Escena de Consolación Ruiz Gil Javier de la Escosura Caballero en Descartes

Licencia Creative Commons by-nc-sa


Icono de iDevice

En la red

 Puedes visitar el siguiente enlace a la actividad ¿A qué distancia está el barco? Este representa otro procedimiento para calcular la distancia a la que está situado un objeto inaccesible. 

 


Matemáticas 3º E.S.O. CeDeC