4.2. Cónicas
Dado que podemos expresar infinitas propiedades geométricas, existen infinitos lugares geométricos diferentes.
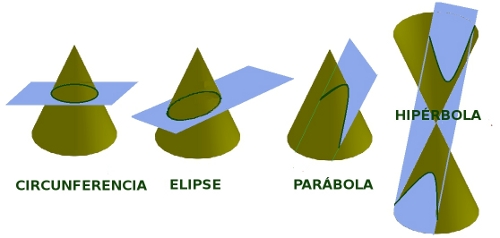
Algunos de los lugares geométricos que aparecen en la vida real son las llamadas cónicas (son las secciones de un cono producidas por un plano. Las puedes ver en la imagen.
 |
|
Cónicas. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa
|
- Circunferencia: el plano es perpendicular al eje del cono.
- Elipse: el plano forma un ángulo con el eje del cono superior al que forma la generatriz con el eje, y es inferior a 90º.
- Parábola: cuando el plano es paralelo a una generatriz del cono.
- Hipérbola: cuando el ángulo que forma el plano con el eje del cono es inferior al que forma la generatriz con dicho eje.
- Cónicas degeneradas: son el caso en que el plano corta al cono en un punto o una o dos rectas.

|
|
Esfera-elipse. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa
|
En la red
 |
En el siguiente enlace puedes ir generando las distintas cónicas en función del ángulo que forma el plano con el eje del cono. |
Importante
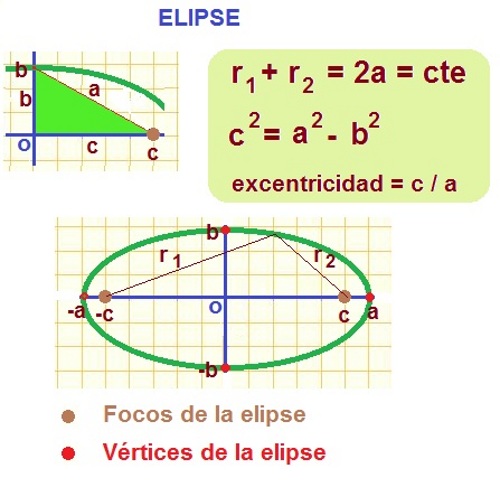
La elipse también se puede definir como el lugar geométrico de los puntos del plano cuya suma de las distancias a dos puntos (llamados focos) es constante (a dicho valor se le representa por 2a).
 |
|
Elipse. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa
|
El valor de a es igual a la longitud del semieje mayor y b la del semieje menor. La distancia de los focos al centro de la elipse se la representa por la letra c.
El valor de la excentricidad (e = c/a) es un valor comprendido entre 0 y 1, de forma que cuanto más pequeño más se acercará a una circunferencia y cuanto mayor sea más achatada es.
Curiosidad
 |
|
Postre. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa
|
- Cuando miramos un objeto con forma de circunferencia desde una cierta distancia fuera de la vertical que pasa por su centro, lo observamos como si fuera una elipse.
- Las trayectorias de los planetas alrededor del Sol tienen forma de elipse.
Anota en tu cuaderno casos de la vida real en los que al mirar objetos de forma circular los observes como elipses. Comenta posteriormente con tus compañeros este tipo de situaciones.
Importante
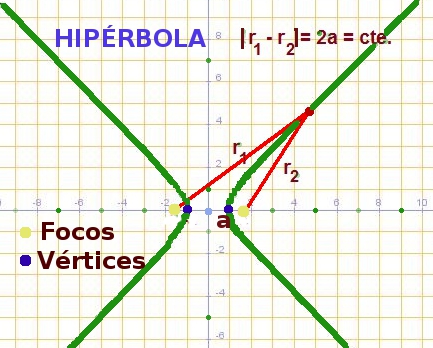
La Hipérbola también se pude definir como el lugar geométrico de los puntos del plano cuya diferencia en valor absoluto de las distancias a dos puntos fijos del plano (llamados focos) es constante.
 |
|
Hipérbola. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa
|
La trayectoria que siguen dos partículas con carga eléctrica del mismo signo (por ejemplo dos electrones); cuando están sometidas exclusivamente a sus fuerzas eléctricas de repulsión, es una hipérbola.
Importante
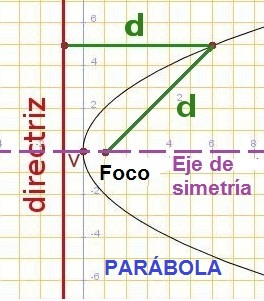
Parábola: Lugar geométrico de los puntos cuya distancia a una recta (llamada directriz) es igual a la distancia a un punto fijo del plano (llamado foco).
 |
|
Parábola. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa
|

|
|
Fuente de Don Benito. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa
|
En la vida real la forma de un chorro de agua es el de una parábola.
Busca otros ejemplos de la vida real cuya forma sea una parábola. Anótalos en tu cuaderno y coméntalos en clase.
En la red
 |
Utiliza el siguiente enlace para dibujar las distintas cónicas moviendo con el cursor el punto P de cada figura. En dicho enlace también podrás ver las ecuaciones matemáticas asociadas a las cónicas, pero este contenido no es de este curso. |