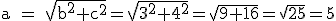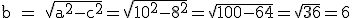3.1 Teorema de Pitágoras
|
|
Enlosado cuadrangular. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa
|
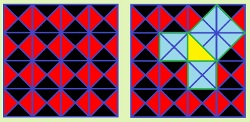
En alguna ocasión te has podido encontrar con un suelo enlosado de forma análoga a la de la parte derecha de la siguiente imagen.
Hemos sombreado algunas de las zonas del enlosado pudiendo observar un triángulo rectángulo y en cada uno de sus lados un cuadrado. Como se puede apreciar, el cuadrado mayor está formado por tantas piezas triangulares como los que hay entre los otros dos juntos. Esto nos lleva a la conclusión de que el área del cuadrado sobre la hipotenusa es igual a la suma de las áreas de los cuadrados sobre los catetos.
Pues bien, esta propiedad no es exclusiva de los rectángulos isósceles, como los de este caso, sino que se puede generalizar a cualquier tipo de triángulo rectángulo. Esto es lo que constituye el "Teorema de Pitágoras".
Importante
Teorema de Pitágoras
En todo triángulo rectángulo la suma de las áreas de los cuadrados construidos sobre sus catetos es igual al área del cuadrado construido sobre su hipotenusa.
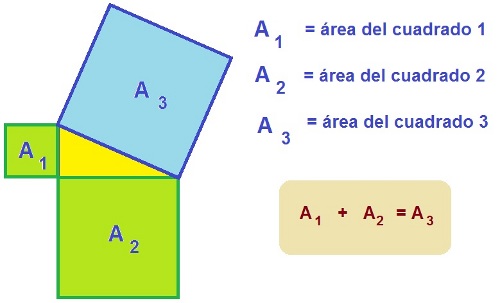
Como consecuencia de que el área del cuadrado es igual al lado al cuadrado, tenemos que: la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, que es otra de las formas en que se expresa dicho teorema.
Si llamamos por tanto b y c a la longitud de los catetos y a al de la hipotenusa, tenemos entonces la fórmula:
a2 = b2 + c2
En la red
| En el siguiente enlace puedes ver una demostración sencilla del teorema de Pitágoras.
|
| En el siguiente enlace puedes ver una visión general del teorema de Pitágoras.
|
Importante
Como consecuencia del teorema de Pitágoras si conocemos dos lados de un triángulo rectángulo podemos calcular el otro.
Dado que a2 = b2 + c2 tendremos: 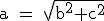 o
o 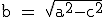
Anota estas fórmulas y dibuja un triángulo rectángulo en tu cuaderno y memorízalas, pero sin olvidar como se obtienen.
 |
¡Buscamos rectángulos!
Busca dos rectángulos que aparezcan en situaciones reales y que estén a tu alcance, como mesas, bancos, pañuelos, folios, etc. y realiza las siguientes actividades.
- Mide el lado y la diagonal de cada uno de los objetos que hayas elegido.
- Realiza un dibujo de cada uno y anota las medidas que has realizado.
- Calcula mediante el teorema de Pitágoras la diagonal de uno de ellos y compara con la medición que has realizado.
- Calcula mediante el teorema de Pitágoras uno de los lados del otro rectángulo y compara con la medición que has realizado.
- Indica las causas por las que se ha podido producir cierta diferencia entre los valores calculados y el de tus medidas.
- Comenta con tus compañeros por qué se produce este tipo de errores.
Curiosidad
Aplicando el teorema de Pitágoras se obtiene que la diagonal d de un cuadrado en función de su lado l, se puede calcular por la fórmula:
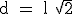
Ten en cuenta que en el cuadrado tendremos d2 = l2 + l2 = 2 l2 . Sacando la raíz cuadrada obtenemos dicha fórmula.