Con una sola ecuación no tenemos bastante
Cambiar para ser equivalente.
Si nos fijamos en la situación anterior, la ecuación que correspondería a la segunda cuestión sería 
. Es la misma que teníamos en la primera cuestión multiplicada por tres. En el segundo caso se ha pedido, y por tanto pagado, el triple que en el primer caso.
Tanto esta ecuación como la de la primera cuestión tienen exactamente las mismas soluciones, por eso reciben un nombre particular, se dice que son equivalentes.
Importante
Dos ecuaciones se llaman equivalentes cuando tienen exactamente las mismas soluciones. Esta definición se amplía también a los sistemas de ecuaciones.
Las tres reglas fundamentales para encontrar ecuaciones o sistemas equivalentes son las siguientes:
1.- Si en una ecuación se multiplican o dividen, por un número distinto de cero, todos los términos de la ecuación, entonces se obtiene una ecuación equivalente.
Por ejemplo, las ecuaciones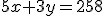 
y 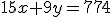son equivalentes.
2.- Si en una ecuación se suma o resta la misma expresión en los dos miembros, la ecuación obtenida es equivalente a la anterior.
Por ejemplo, las ecuaciones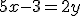 
y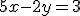 
(hemos sumado 3 en los dos miembros y restado 2y) son equivalentes.
3.- Si en un sistema, a una ecuación se le suma o resta la otra multiplicada por cualquier número, distinto de cero, el sistema que se obtiene es equivalente al anterior.
Por ejemplo, el sistema 
es equivalente al sistema 
, pues a la segunda ecuación le hemos sumado la primera multiplicada por 2.
Realiza el test que aparece en la siguiente ventana. Una vez que termines en una pantalla pulsa el botón con la flecha en la parte inferior derecha.
Ecuaciones y sistemas equivalentes. Applet creado por Jose Muñoz Santonja.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0