Teorema de Thales

Como puedes ver en la figura, hemos troceado el triángulo OCC' de forma que la base la hemos dividido en tres partes iguales de 2m cada una.

Trazando las verticales por cada una de las divisiones obtenemos los puntos A', B' y C' que determinan tres segmentos de igual longitud (2,5 m).

Por tanto podemos observar que se cumple una proporción entre la longitud de los distintos segmentos que podemos formar en el lado OC' del triángulo y sus correspondientes al lado OC, tal y como puedes comprobarlo en las proporciones que se indican a la derecha de la figura.

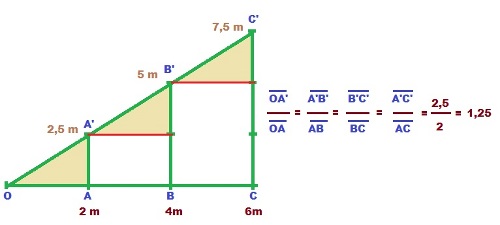
Triángulo troceado

Triángulo troceado. Arturo Mandly (CC by sa)

Pues bien, esta propiedad de proporcionalidad se puede generalizar y es lo que constituye el teorema de Thales.

Importante

Teorema de Thales: Si dos rectas cualesquiera son cortadas por rectas paralelas, los segmentos que determina en una de las rectas son proporcionales a los segmentos correspondientes de la otra.

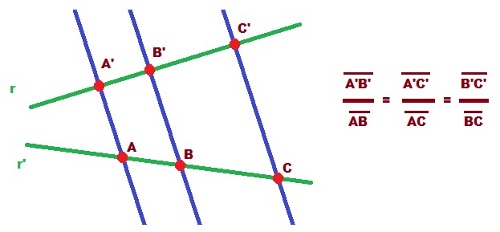
Teorema de Thales

Teorema de Thales. Arturo Mandly (CC by sa)

Este teorema nos permite calcular, por tanto, la longitud de un segmento si conocemos su correspondiente en la otra recta y la proporción entre ambos.

Anota en tu cuaderno el enunciado del teorema de Thales y el dibujo que hemos incluido.

Tarea

Utilizamos la regla

Traza dos rectas r y r' cualesquiera (que no sean paralelas) y realiza las siguientes actividades:

Traza tres puntos A, B y C sobre la recta r y que estén separados 2 cm A y B, y 3 cm B y C.

Traza tres rectas paralelas entre sí por los puntos A, B y C, y determina los puntos de corte correspondientes en la recta r', A', B' y C'.

Mide cuidadosamente los distintos segmentos que se forman y comprueba que se cumple el teorema de Thales.

Si trazaras un segmento de 6 cm en la recta r y trazaras dos paralelas por sus extremos a las anteriores ¿cuánto mediría el segmento que se formaría en la recta r' ?

Realiza un informe con los resultados que has obtenido y comenta los resultados con tus compañeros.

Como consecuencia del teorema de Thales, la proporción entre dos de los segmentos obtenidos por las rectas paralelas en una de las rectas es la misma que sus correspondientes a las intersecciones en la otra.

En la siguiente escena puedes comprobar este resultado.

Teorema de Thales. Budigali. (CC by sa)