Teoremas basados en los triángulos rectángulos
Además del teorema de Pitágoras, existen tres teoremas importantes sobre los triángulos rectángulos que permiten resolver ciertos problemas geométricos de una forma rápida. Estos teoremas son los siguientes:
|
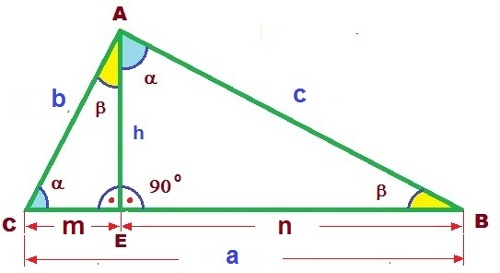
Triángulo rectángulo proyecciones. Imagen de Arturo Mandly en Flickr
Licencia Creative Commons by-nc-sa
|
- Teorema del cateto: relaciona los catetos (b y c) con la hipotenusa (a) y las proyecciones de los catetos sobre la hipotenusa (m y n).
- Teorema de la altura: relaciona la altura (h) con las proyecciones de los catetos sobre la hipotenusa (m y n)
- Teorema sobre la altura y la hipotenusa: relaciona la hipotenusa (a) y altura (h) con los catetos (b y c).
Importante
Teorema del cateto
El cuadrado de un cateto es igual al producto de la hipotenusa por la proyección de dicho cateto sobre la hipotenusa.
Como consecuencia tenemos las siguientes fórmulas:
- b2 = m·a
- c2 = n·a
siendo a = m + n y m la proyección del cateto b sobre la hipotenusa y n la del cateto c, tal y como se puede observar en el triángulo anterior.
La media proporcional (o geométrica) de dos números es la raíz cuadrada de su producto. Esto nos indica que; si extraemos la raíz cuadrada a cada término de las dos expresiones, tenemos que los catetos son la media proporcional de sus proyecciones y la hipotenusa.
Estas fórmulas nos permiten calcular los catetos, conocidas sus proyecciones o bien calcular un cateto conocida su proyección y la hipotenusa.
En el siguiente ejemplo puedes desplazar el vértice C y comprobar que se verifica la fórmula del teorema del cateto.
Teorema del Cateto. Basado en Demostración del Teorema de Pitágoras por semejanza Compartida por José Manuel Infante Infante CC by sa
Importante
Teorema de la altura
El cuadrado de la altura sobre la hipotenusa de un triángulo rectángulo es igual al producto de las proyecciones de sus catetos sobre la hipotenusa.
Es decir que h2 = m·n
Este teorema nos permite calcular la altura sobre la hipotenusa de un triángulo rectángulo si conocemos las proyecciones de los catetos sobre la hipotenusa.
También nos dice que la altura es la media proporcional (o geométrica) de las proyecciones.
En el siguiente ejemplo puedes desplazar el vértice C y comprobar que se cumple el teorema de la altura.
Teorema de la altura. Basado en Demostración del Teorema de Pitágoras por semejanza Compartida por José Manuel Infante Infante CC by sa
Importante
Teorema sobre la hipotenusa y la altura
Podemos expresarlo mediante la fórmula a·h = b·c y nos permitirá calcular la altura de un triángulo rectángulo en función de la hipotenusa y sus catetos.
Si dividimos ambos miembros de la fórmula anterior por 2, puedes observar que cada miembro representa el área del triángulo rectángulo.
Comprueba lo aprendido
Solución
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0