Saltar la navegación

Triángulos semejantes

Importante

Triángulos semejantes

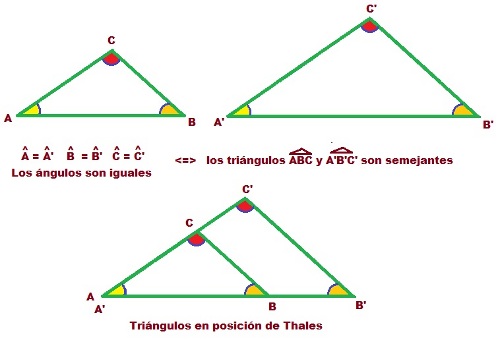
Dos triángulos son semejantes si tienen los mismos ángulos.

Si hacemos coincidir los vértices de los dos triángulos que tengan el mismo ángulo, obtenemos lo que se llama posición en Thales de los triángulos semejantes.

Triángulos semejantes. Arturo Mandly. (CC by sa)

Comprueba lo aprendido

Escribe en tu cuaderno las siguientes afirmaciones e indica si son verdad o no y por qué.

Pregunta 1

Todos los triángulos isósceles son semejantes entre sí.

Sugerencia

Ten en cuenta que no tienen por qué tener el mismo ángulo que es distinto.

Pregunta 2

Todos los triángulos equiláteros son semejantes entre sí.

Sugerencia

Observa cuanto miden sus ángulos.

Pregunta 3

Dos ángulos de un triángulo miden 60º y 40º; los de otro miden 80º y 40º. Por tanto, ambos triángulos son semejantes.

Sugerencia

Calcula cuanto mide el otro ángulo de cada triángulo (ten en cuenta que la suma de los ángulos de cualquier triángulo es 180º)

Tarea

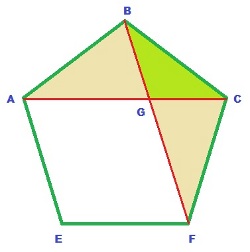
¡Pentágonos!

Dibuja en tu cuaderno un pentágono regular como el de la figura (no hace falta que sea totalmente exacto), del tamaño que tú prefieras y resuelve las siguientes cuestiones:

  • Determina cuánto mide el ángulo del vértice E del pentágono.
  • Determina si el triángulo con vértices en los puntos A,B y C es semejante al de vértices en los puntos A, B y G.
  • Determina si el triángulo con vértices los puntos A,B y C es semejante al de vértices en los puntos B, C y G.

Importante

Como has visto cuando colocamos dos triángulos en posición de Thales, si prolongáramos todos los segmentos, obtendríamos precisamente las condiciones en las que se cumple el teorema de Thales: dos rectas cortadas a su vez por rectas paralelas entre sí.

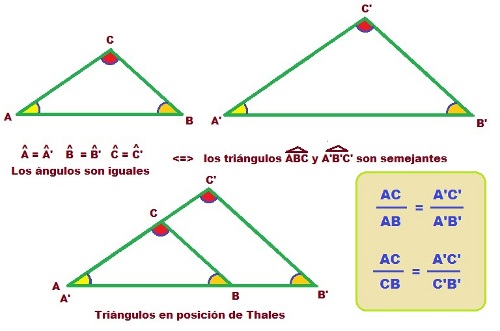
Como consecuencia; podemos establecer que la proporción entre dos lados cualesquiera de uno de los dos triángulos, es igual a la misma proporción entre los lados correspondientes en el otro triángulo.

Esta propiedad nos va a permitir calcular un lado de un triángulo a partir de otro conocido y las medidas de los lados de otro triángulo semejante a él. En el siguiente apartado vamos a aplicarla a la resolución de problemas de cálculos de longitudes. 

Comprueba lo aprendido

Pregunta

¿Cuál es la longitud del lado  CC'?

Sugerencia

Aplica el teorema de Thales a los dos triángulos que son semejantes.

Respuestas

a) 2,15 m

b) 2,71 m

c) 2,51 m

d) 2,81 m

Retroalimentación

Comprueba lo aprendido

Pregunta

¿Cuánto mide el lado AC ?

Sugerencia

Aplica el teorema de Thales a los dos triángulos semejantes.

Respuestas

a) 3,5 m

b) 2,5 m

c) 4,5 m

Retroalimentación

Comprueba lo aprendido

Indica si son verdaderas o falsas las siguientes afirmaciones. Copialas y razona la respuesta en tu cuaderno.

Pregunta 1

Si construimos un triángulo equilátero cuya altura sea el doble de la de otro triángulo equilátero, su lado también medirá el doble.

Sugerencia

Puedes colocar ambos triángulos en posición de Thales.

Pregunta 2

Si reducimos a la mitad las diagonales de un rombo, su lado queda reducido a la cuarta parte.

Sugerencia

Divide el rombo en triángulos iguales.

Pregunta 3

A un triángulo rectángulo cuyos catetos miden 8 cm y 4 cm los aumentamos 4 cm, por tanto ambos triángulos son semejantes entre sí.

Sugerencia

Calcula la proporción entre los catetos en ambos triángulos.

Curiosidad

 

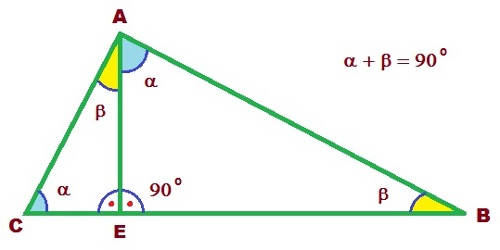
Si trazamos la altura de un triángulo rectángulo tomando como base a la hipotenusa, obtenemos otros dos triángulos rectángulos que a su vez son semejantes a él.

En la red
Si deseas ampliar información sobre los triángulos semejantes puedes visitar el siguiente enlace. 

 

Seguir practicando

¿Serás capaz de resolver todos los ejercicios del documento adjunto? Inténtalo y comprueba si lo has conseguido.