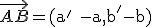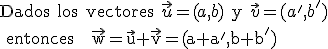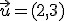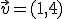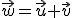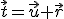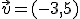Anota en tu cuaderno las siguientes definiciones y ejercicios de este apartado.
Si representamos un vector en un sistema de coordenadas cartesianas de tal forma que su origen se haga coincidir con el del sistema, podemos asignarle las coordenadas del extremo del vector. A estas coordenadas también se les llama componentes del vector.
Desplaza el vértice A del vector para observar el cambio de las componentes del vector