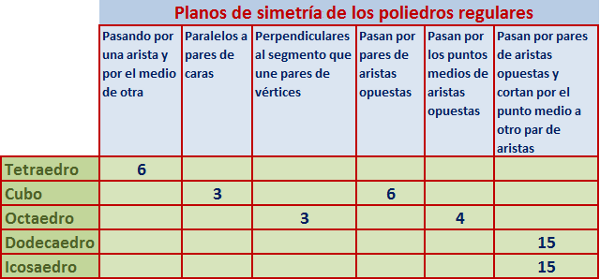
Los poliedros regulares son aquellos que tienen sus caras y ángulos iguales. Sólo existen cinco poliedros regulares: tetraedro, cubo, octaedro, dodecaedro e icosaedro.
Sus caras son polígonos regulares: triángulos equiláteros (en el tetraedro, octaedro e icosaedro), cuadrados (en el cubo) y pentágonos (en el dodecaedro).
Antes de proceder a estudiar los planos de simetría de estos poliedros mira en el siguiente enlace algunas aplicaciones, usos artísticos y cómo aparecen en la naturaleza.
Anota en tu cuaderno algunas de las partes del vídeo relativas a los poliedros regulares que te han resultado interesantes.
Anota la siguiente tabla en tu cuaderno. En ella se recogen los distintos tipos de planos de simetría que tienen los poliedros regulares y el número de ellos.
 |
Vamos a comprobar uno de los planos de simetría del cubo, para lo cual debes realizar las siguientes actividades:
Los poliedros regulares pueden obtenerse mediante los llamados caleidoscopios poliédricos consistentes en pirámides construidas con espejos.
En el siguiente vídeo se presenta una visión general sobre este tipo de caleidoscopios.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0
