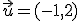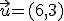Importante
Traslación
Se define traslación producida por un vector libre 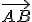 a la transformación que hace corresponder a todo punto P del plano otro punto P' de tal forma que
a la transformación que hace corresponder a todo punto P del plano otro punto P' de tal forma que 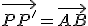
Para obtener las coordenadas del punto P' basta con sumarle a las de P las componentes del vector 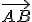
En la siguiente escena puedes obtener la traslación del segmento de extremos los puntos P y Q producida por el vector de extremos los puntos A y B. Mueve los puntos A y B para cambiar el vector que produce la traslación, o los puntos P y Q para modificar el segmento a transformar.
Comprueba como ambos segmentos se mantienen siempre paralelos y con la misma longitud.
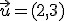 determinar las coordenadas de los puntos obtenidos por traslación mediante dicho vector de los siguientes puntos:
determinar las coordenadas de los puntos obtenidos por traslación mediante dicho vector de los siguientes puntos: