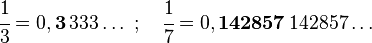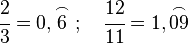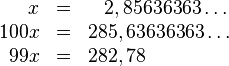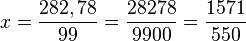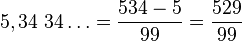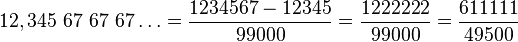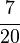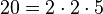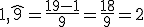Ya hemos visto cómo una fracción se puede expresar en forma decimal.

Ahora vamos a realizar el proceso inverso, es decir, vamos a obtener una fracción que se corresponda con un número expresado en forma decimal sea exacto, periódico puro o periódico mixto.

Número decimal periódico

De Wikipedia, la enciclopedia libre (Redirigido desde «Número decimal periodico»)

Un número decimal periódico es un número racional caracterizado por tener un período (cifras que se repiten indefinidamente) en su expansión decimal. Este período puede constar de una o varias cifras, como:

$\cfrac{1}{3} = 0,\boldsymbol{3}\,333\dots \; ; \quad \cfrac{1}{7} = 0,\boldsymbol{142857}\,142857\dots$

El período se puede expresar escribiendo un arco encima de las cifras repetidas, por ejemplo:

$\cfrac{2}{3} = 0, \overset{\frown}{6} \; ; \quad \cfrac{12}{11} = 1, \overset{\frown}{09}$

Tipos de números periódicos

Número periódico puro: Cuando inmediatamente después de la coma hay una o más cifras que se repiten.
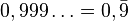
- Ejemplo: $0,999\dots = 0,\bar{9}$
Número periódico mixto (también llamado semiperiódico): Cuando después de la coma hay una o más cifras que no se repiten, seguidas por una o más cifras que sí se repiten.
- Ejemplo: 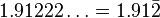$1.91222\dots = 1.91 \bar{2}$ , en donde 91 es el anteperíodo.

Fracción correspondiente a un número periódico

Una fracción puede dar un número decimal periódico:

\begin{array}{l} \cfrac{1}{9} = 0,111111111111...\\ \cfrac{1}{7} = 0,142857142857...\\ \cfrac{1}{3} = 0,333333333333...\\ \cfrac{2}{27} = 0,074074074074...\\ \cfrac{7}{12} = 0,58333333333... \end{array}

Dado un número periódico en su representación decimal, es posible encontrar la fracción que lo produce (fracción generatriz). Ejemplo:

\begin{array}{rcll} x & = & 0,333333\ldots\\ 10x & = & 3,333333\ldots & \text{(multiplicando por 10 ambos miembros)} \\ 9x & = & 3 & \text{(restando segunda fila menos primera fila)} \\ \\ x & = & \cfrac{3}{9} = \cfrac{1}{3} & \text{(simplificando)} \end{array}

Otro ejemplo:

\begin{array}{rcl} x & = & \;\;\; 2,85636363\ldots \\ 100x & = & 285,63636363\ldots \\ 99x & = & 282,78 \end{array}

x = \frac{282,78}{99} = \frac{28278}{9900} = \frac{1571}{550}

El procedimiento anterior es general y permite enunciar las siguientes reglas:

Número periódico puro: La fracción de un número decimal periódico puro tiene:

numerador: la diferencia entre la parte anterior al período seguida del período (todo escrito sin la coma, de corrido, como un único número entero) menos la parte anterior al período.

denominador: tantos 9 como cifras tiene el período

Ejemplo:

5,34\ 34\dots = \frac{534-5}{99} = \frac{529}{99}

Número periódico mixto: La fracción de un número decimal periódico mixto tiene:

numerador: la diferencia entre la parte anterior al período seguida del período (todo escrito sin la coma, de corrido, como un único número entero) menos la parte anterior al período.

denominador: tantos 9 como cifras tiene el período, seguidos de tantos 0 como cifras tiene la parte no periódica.

Ejemplo:

12,345\ 67\ 67\ 67\dots = \frac{1234567-12345}{99000} = \frac{1222222}{99000} = \frac{611111}{49500}

Tipo de número periódico resultante

Dada una fracción irreducible (es decir, en la que numerador y denominador son primos entre sí, y por tanto no se puede simplificar más) es sencillo saber si corresponde a un número periódico puro, mixto, o es un decimal exacto, sin necesidad de hacer la división: