juantiagues. Mar de Camelias (CC BY-SA)

Pero... ¿y si falta alguien? ¿Qué hacemos? ¿Cómo lo resolvemos?

En numerosas ocasiones, las ecuaciones de segundo grado no quedan completas, sino que falta algún término. Sin ir más lejos, el ejemplo con el que empezamos el apartado anterior, ¿recuerdas?, el del expositor que quería comprar Juan que ocupara 6 metros cuadrados, nos daba como ecuación:

x² = 6 ,

y si lo expresamos como las ecuaciones generales, nos quedaría:

x² - 6 = 0,

o sea, una ecuación en la que falta el término con x; falta b.

Estos casos podríamos resolverlos utilizando la fórmula y dándole al término que faltara el valor 0.

Por ejemplo, en la ecuación que acabamos de poner,

x² - 6 = 0,

si usáramos la fórmula tendríamos que a = 1, b = 0, pues no hay término con x y c = -6. Sustituyendo nos quedaría:

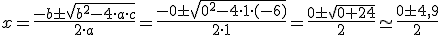
Luego tendríamos que una solución es 4,9/2 = 2,45 y la otra - 4,9/2 = -2,45; aunque en el contexto de nuestro problema, como x era la longitud del lado del expositor, la única solución válida sería 2,45 metros.

Pero seguro que estás pensando, ¿y para qué hace todo esto? ¡Si se puede hacer mucho más fácil!  ¡Si sólo hay que hacer la raíz cuadrada de 6!, ¿verdad?