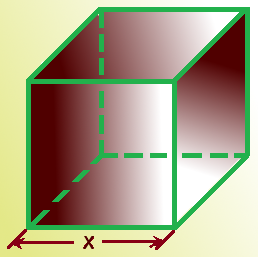
Cubo. Imagen de Arturo Mandly

Del cubo de la figura podemos expresar su volumen y su superficie total en función de la medida de sus aristas (x):

Volumen V(x) = x³

Superficie total S(x) = 6x²

Estas fórmulas forman parte de las expresiones algebraicas más sencillas llamadas monomios en las cuales el valor particular se obtiene cuando sustituimos la letra x por un valor concreto. Así por ejemplo si x = 4 cm, tendremos que V = 4³ = 64 cm³ y S = 6·4² = 96 cm².

A partir de estas expresiones, se pueden construir otras también sencillas llamadas polinomios y a partir de ellos a su vez otras más complejas.

Los monomios están formados por una parte numérica y por otra literal que puede contener una o varias letras que denominamos variables.

 Definiciones

• Un polinomio es una "suma de monomios". Cada uno de los sumandos que aparecen se denomina término del polinomio y cada uno es un monomio. El grado del polinomio es el grado mayor de los monomios que lo forman.

Ejemplos:2x²-7x+1 (grado 2), 8x-5x⁴+3 (grado 4), 9 (polinomio de grado 0). Pero 3x²-5x^-2 (no tiene grado ya que no es un polinomio, hay una potencia de x con exponente negativo).

• El valor numérico de un polinomio para un determinado número, es el número que se obtiene sustituyendo x por dicho número. Ejemplo: si P(x) = 2x³-5x+4 , P(2) = 2·2³-5·2+4 = 2·8-10+4 = 10.

• El número a es raíz o cero de un polinomio P(x) si P(a)=0.

Ejemplos:

1. P(x) = x²-3x+2 tiene por raíces x=1 y x=2.

2. P(x) = x²-2x+1 = 0 tiene por única raíz x = 1, pues x²-2x+1 = (x-1)² (en este caso se dice que la raíz es doble).

3. P(x)= x²+1 = 0 no tiene ninguna raíz real, pues el cuadrado de todo número real es positivo (así x²+1>0).

Simplificación de expresiones algebraicas, reduciendo términos semejantes.

Esta aplicación permite practicar la tarea de simplificar una expresión algebraica reduciendo términos semejantes.

gtinoco. Términos semejantes. (CC by sa)

El botón "Otro" genera un nuevo ejercicio.

La casilla de control "Ordena", ordena los términos de la expresión de acuerdo al exponente de la variable.

La casilla de control "Simplificación" muestra la reducción de términos semejantes.