 |
|
Producto de dos polinomios.
Imagen de Arturo Mandly
|
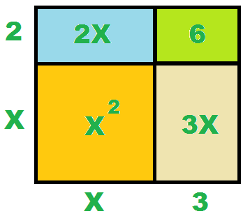
Aquí tienes una aplicación geométrica del producto de dos polinomios:
(x +3)·(x+2) = x2 + 5x +6. ¿Lo recuerdas?
Viendo el área total del rectángulo,
(x+3)·(x+2)
observábamos que ésta era la misma que si se partía en trocitos y se sumaban éstos:
x2 + 2x + 3x +6
Pues bien esta igualdad algebraica es cierta sea cual sea el valor de x. Siempre es verdad.
Una Identidad es una igualdad algebraica, esto es, una igualdad en la que aparecen números y letras que siempre se cumple, sean cuales sean los valores de las incógnitas.
Vamos a pensar en el siguiente ejemplo sencillo:
Mi amiga Ana va a abrir una nueva tienda en un centro comercial y ha pedido presupuesto para las estanterías que piensa poner. Le han dado un presupuesto en el que cada estantería cuesta 68 €. En total, con los gastos de montaje de 140 € incluidos, la factura sería de 412 €.
¿Sabrías decir cuántas estanterías piensa poner Ana?
Una ecuación es una igualdad algebraica que es cierta para algunos valores de las incógnitas y falsa para otros.
Por tanto, la diferencia entre identidad y ecuación es que la identidad siempre es cierta, mientras que la ecuación no.
El valor o valores de la incógnita que hacen que la igualdad se cumpla se llaman solución de la ecuación.
Vamos a ver un ejemplo en el que tenemos que distinguir entre una igualdad o una ecuación. Para ello tendremos que ver si la igualdad se cumple para cualquier valor de x o no.
Indica si la igualdad 2(x+4) + 3x = 5x + 8 es identidad o ecuación.
Indica si la igualdad 2(x+5) - 3x = x + 10 es una identidad o una ecuación.
¿Eres capaz de resolver 5 cuestiones consecutivas correctamente? Observa los vídeos explicativos y realiza los ejercicios propuestos.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0
