A veces, las sucesiones se dan de forma recurrente. Por ejemplo, en la sucesión 8, 13, 18, 23, ... podemos ver que cada término se obtiene sumando 5 unidades al anterior. Podemos por tanto decir que 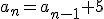 . Pero, aún así, es fácil encontrar un término general, en concreto,
. Pero, aún así, es fácil encontrar un término general, en concreto, 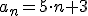 . Sin embargo, hay otras sucesiones recurrentes en las que no es tan fácil encontrar el término general, por ejemplo, 1, 5, 14, 30, 55, 91, ... tiene como ley de recurrencia
. Sin embargo, hay otras sucesiones recurrentes en las que no es tan fácil encontrar el término general, por ejemplo, 1, 5, 14, 30, 55, 91, ... tiene como ley de recurrencia 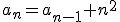 .
.
Dentro de las sucesiones recurrentes la más conocida es la Sucesión de Fibonacci, que vimos en el vídeo de la introducción. En esa sucesión, 1, 1, 2, 3, 5, 8, 13, ... cada término, a partir del tercero, se calcula sumando los dos anteriores. Es decir, su ley de formación sería 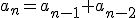 . Aunque puede parecer que es una sucesión extraña vamos a ver que tiene muchas aplicaciones.
. Aunque puede parecer que es una sucesión extraña vamos a ver que tiene muchas aplicaciones.
