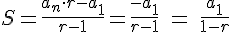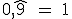Siempre que vamos sumando los términos de una progresión, el valor de la suma va aumentando; de forma positiva o negativa según el signo de los términos. En muchos casos, cuando se añade un número indeterminado de términos, la suma va haciéndose infinita, Pero ¿ocurre esto siempre?
La respuesta es no. Piensa en la tarea que has resuelto en el apartado anterior. Habrás comprobado que el balón, en los primeros cinco botes recorre una gran parte del campo, pero en los siguientes cinco avanza muy poco (y avanzará menos si sigue menguando la distancia recorrida en cada bote). En general, cuando tenemos una progresión geométrica en la que la razón es menor que la unidad, los términos de la progresión se van haciendo cada vez más pequeños. Veamos el siguiente ejemplo:
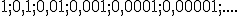
Es evidente que podemos considerar que a partir de un determinado momento los términos valen prácticamente cero.
Por ello, en las progresiones geométricas podemos hallar la suma de todos los términos de la progresión. Basta considerar en la fórmula que dedujimos en el apartado anterior que para un valor n suficientemente grande, an=0. De esa forma, la suma de los infinitos términos de una progresión geométrica de razón menor de la unidad viene dada por la fórmula: