Importante
Se llama progresión geométrica a toda sucesión en la que un término se obtiene del anterior multiplicado por un valor constante, r, que se llama razón. Es decir, se verifica la igualdad:
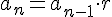
Si 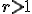 y
y 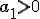 , cada término es mayor que el anterior, por lo tanto, la progresión es una sucesión creciente. Por ejemplo, 3, 6, 12, 24, 48, ....
, cada término es mayor que el anterior, por lo tanto, la progresión es una sucesión creciente. Por ejemplo, 3, 6, 12, 24, 48, ....
Si 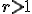 y
y 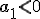 ,
cada término es menor que el anterior, por lo tanto, la progresión es
una sucesión decreciente. Por ejemplo, -1, -5, -25, -125, -625, ....
,
cada término es menor que el anterior, por lo tanto, la progresión es
una sucesión decreciente. Por ejemplo, -1, -5, -25, -125, -625, ....
Si 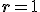 , todos los términos son iguales y la sucesión es constante. Por ejemplo, 3, 3, 3, 3, .....
, todos los términos son iguales y la sucesión es constante. Por ejemplo, 3, 3, 3, 3, .....
En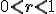 ; si el primer término es positivo, la sucesión es decreciente, por ejemplo, 32, 16, 8, 4, 2, ...; mientras que si el primer término es negativo, la sucesión es creciente, por ejemplo, -81, -27, -9, -3, -1, ...
; si el primer término es positivo, la sucesión es decreciente, por ejemplo, 32, 16, 8, 4, 2, ...; mientras que si el primer término es negativo, la sucesión es creciente, por ejemplo, -81, -27, -9, -3, -1, ...
Si 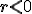 , unos términos de la sucesión son positivos y los otros negativos, por lo que la progresión es oscilante y suelen llamarse progresiones alternadas.
, unos términos de la sucesión son positivos y los otros negativos, por lo que la progresión es oscilante y suelen llamarse progresiones alternadas.

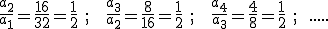
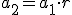
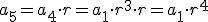
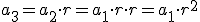
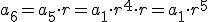
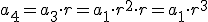
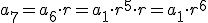
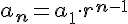
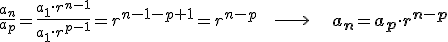
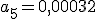 y
y 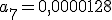 .
.
