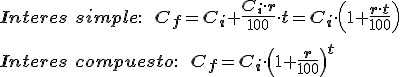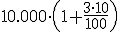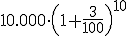Todo por el interés. ppmuñoz(CC by sa)

Una de las cosas más corrientes en nuestro mundo son las relaciones financieras con los bancos. Rara es la familia que no tiene algún tipo de cuenta en un banco, bien porque se tenga algún dinero invertido o algún plan de pensiones, o bien, como ocurre en muchos casos, porque se haya pedido un préstamo para adquirir una vivienda, algún vehículo o incluso afrontar un gasto extra como una boda o un viaje. Lo cierto es que prácticamente todo el mundo sabe lo que es un interés bancario y, casualmente, esos intereses tienen mucho que ver con las progresiones.

En general, cuando una cantidad monetaria cambia de manos mediante un préstamo o imposición, es necesario devolver la cantidad inicial mas otra cantidad que corresponde a los beneficios que quiere obtener el que presta el dinero. Esa cantidad se llama interés, y suele darse en tanto por ciento.

Hay dos tipos de interés: el que se recoge año a año, que recibe el nombre de interés simple, y otro que se va incorporando a la cantidad inicial y sólo se recoge al final (por lo que esa cantidad también incrementa, cada año, la cantidad inicial). Este segundo tipo recibe el nombre de interés compuesto.

Veamos un ejemplo numérico. Consideremos que ingresamos 12.000 euros en una entidad bancaria y nos dicen que nos van a dar un 4% de interés. Veamos cómo varía la cantidad que tenemos según el tipo de interés. Representamos por C_i el capital inicial que tenemos al principio del año y por C_f la cantidad final que tenemos en un determinado momento.

Si representamos por r el tanto por ciento que nos ofrecen de interés, podemos apreciar que en el primer caso nos encontramos con una progresión aritmética cuya diferencia es 480, equivalente a 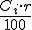. En el caso del interés compuesto, cada año se multiplica por 1,04 (ya que se haya el 4% de la cantidad inicial en ese año). Luego tenemos una progresión geométrica donde la razón es .

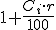Por eso, las fórmulas para los distintos intereses suponiendo que tenemos un capital 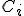invertido al r% durante t años son:

En el siguiente enlace (¿Capitalización de intereses?), tienes un estudio comparativo sobre lo que se consigue poniendo una cierta cantidad al 4%, según se haya colocado con interés simple (sin amortización) o compuesto (con amortización).

Puedes modificar el número de años que se tiene invertido para que compruebes que cuántos más años, mayor es la diferencia.